Shift Theorem
The shift theorem says that a delay of ![]() samples
in the time domain corresponds to a multiplication by
samples
in the time domain corresponds to a multiplication by
![]() in the frequency domain:
in the frequency domain:
Proof:
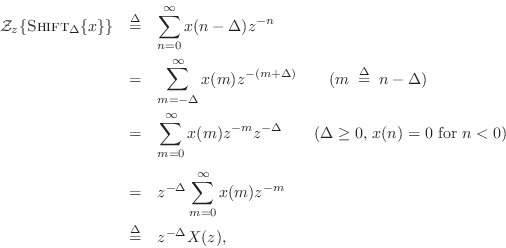
where we used the causality assumption ![]() for
for ![]() .
.
Next Section:
Convolution Theorem
Previous Section:
Complete Response




















