A Short-Cut to Controller Canonical Form

When converting a transfer function to state-space form by hand, the step of pulling out the direct path, like we did in going from Eq.(G.13) to Eq.(G.14), can be bypassed [28, p. 87].

Figure: Direct-form-II realization of Eq.(G.7). Note that this form has a delay-free path from input to output.

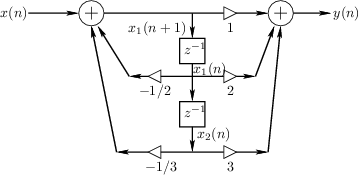Figure G.2 gives the standard direct-form-II structure for a second-order IIR filter. Unlike Fig.G.1, it includes a direct path from the input to the output. The filter coefficients are all given directly by the transfer function, Eq.(G.13).

This form can be converted directly to state-space form by carefully observing all paths from the input and state variables to the output. For example, reaches the output through gain 2 on the right, but also via gain on the left and above. Therefore, its contribution to the output is , as obtained in the DF-II realization with direct-path pulled out shown in Fig.G.1. The state variable reaches the output with gain , again as we obtained before. Finally, it must also be observed that the gain of the direct path from input to output is .

Sign in