The term sinusoid means a waveform of the type
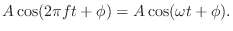 |
(A.1) |
Thus, a sinusoid may be defined as a
cosine at amplitude
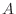
,
frequency

, and phase

. (See [
84] for a fuller
development and discussion.)
A sinusoid's
phase 
is in radian units. We may call
the
instantaneous phase, as distinguished from the
phase offset 
. Thus, the ``phase'' of a sinusoid
typically refers to its phase offset. The
instantaneous
frequency of a sinusoid is defined as the
derivative of the
instantaneous phase with respect to time (see [
84] for more):
A
discrete-time sinusoid is simply obtained from a continuous-time
sinusoid by replacing

by
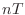
in Eq.

(
A.1):
Next Section: SpectrumPrevious Section: Units
![$\displaystyle f(t) \isdef \frac{d}{dt} \theta(t) = \frac{d}{dt} \left[\omega t + \phi\right] = \omega
$](http://www.dsprelated.com/josimages_new/filters/img1302.png)
![$\displaystyle f(t) \isdef \frac{d}{dt} \theta(t) = \frac{d}{dt} \left[\omega t + \phi\right] = \omega
$](http://www.dsprelated.com/josimages_new/filters/img1302.png)