State Space Simulation in Matlab
Since matlab has first-class support for matrices and vectors, it is quite simple to implement a state-space model in Matlab using no support functions whatsoever, e.g.,
% Define the state-space system parameters: A = [0 1; -1 0]; % State transition matrix B = [0; 1]; C = [0 1]; D = 0; % Input, output, feed-around % Set up the input signal, initial conditions, etc. x0 = [0;0]; % Initial state (N=2) Ns = 10; % Number of sample times to simulate u = [1, zeros(1,Ns-1)]; % Input signal (an impulse at time 0) y = zeros(Ns,1); % Preallocate output signal for n=0:Ns-1 % Perform the system simulation: x = x0; % Set initial state for n=1:Ns-1 % Iterate through time y(n) = C*x + D*u(n); % Output for time n-1 x = A*x + B*u(n); % State transitions to time n end y' % print the output y (transposed) % ans = % 0 1 0 -1 0 1 0 -1 0 0The restriction to indexes beginning at 1 is unwieldy here, because we want to include time
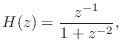
NUM = [0 1]; DEN = [1 0 1]; y = filter(NUM,DEN,u) % y = % 0 1 0 -1 0 1 0 -1 0 1To eliminate the unit-sample delay, i.e., to simulate
[A,B,C,D] = tf2ss([1 0 0], [1 0 1]) % A = % 0 1 % -1 -0 % % B = % 0 % 1 % % C = % -1 0 % % D = 1 x = x0; % Reset to initial state for n=1:Ns-1 y(n) = C*x + D*u(n); x = A*x + B*u(n); end y' % ans = % 1 0 -1 0 1 0 -1 0 1 0Note the use of trailing zeros in the first argument of tf2ss (the transfer-function numerator-polynomial coefficients) to make it the same length as the second argument (denominator coefficients). This is necessary in tf2ss because the same function is used for both the continous- and discrete-time cases. Without the trailing zeros, the numerator will be extended by zeros on the left, i.e., ``right-justified'' relative to the denominator.
Next Section:
Other Relevant Matlab Functions
Previous Section:
Matlab Direct-Form to State-Space Conversion




















