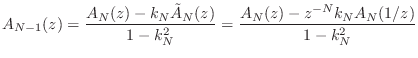DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Step-Down Procedure

Let $ A_N(z)$ denote the $ N$th-order denominator polynomial of the recursive filter transfer function $ H(z)=B(z)/A_N(z)$:

$\displaystyle A_N(z) \isdef 1 + a_{N,1}\,z^{-1}+ a_{N,2}\, z^{-2}+ \cdots + a_{N,N-1}\,z^{-(N-1)} + a_{N,N}\,z^{-N} \protect$ (9.4)

We have introduced the new subscript $ N$ because the step-down procedure is defined recursively in polynomial order. We will need to keep track of polynomials orders between 1 and $ N$.

In addition to the denominator polynomial $ A_N(z)$, we need its flip:

$\displaystyle \tilde{A}_N(z)$ $\displaystyle \isdef$ $\displaystyle z^{-N}A_N(1/z)$  
  $\displaystyle =$ $\displaystyle a_{N,N} + a_{N,N-1}\,z^{-1}+ a_{N,N-2}\, z^{-2}+ \cdots$  
    $\displaystyle \quad + a_{N,2}\,z^{-(N-2)} + a_{N,1}\,z^{-(N-1)} + z^{-N} \protect$ (9.5)

The recursion begins by setting the $ N$th reflection coefficient to $ k_N = a_{N,N}$. If $ \left\vert k_N\right\vert\geq 1$, the recursion halts prematurely, and the filter is declared unstable. (Equivalently, the polynomial $ A_N(z)$ is declared non-minimum phase, as defined in Chapter 11.)

Otherwise, if $ \left\vert k_N\right\vert<1$, the polynomial order is decremented by 1 to yield $ A_{N-1}(z)$ as follows (recall that $ A_N(z)$ is monic):

$\displaystyle A_{N-1}(z) = \frac{A_N(z) - k_N \tilde{A}_N(z)}{1-k_N^2} = \frac{A_N(z) - z^{-N} k_N A_N(1/z)}{1-k_N^2} \protect$ (9.6)

Next $ k_{N-1}$ is set to $ a_{N-1,N-1}$, and the recursion continues until $ k_1=a_{1,1}$ is reached, or $ \left\vert k_i\right\vert\geq 1$ is found for some $ i$.

Whenever $ \left\vert k_m\right\vert=1$, the recursion halts prematurely, and the filter is usually declared unstable (at best it is marginally stable, meaning that it has at least one pole on the unit circle).

Note that the reflection coefficients can also be used to implement the digital filter in what are called lattice or ladder structures [48]. Lattice/ladder filters have superior numerical properties relative to direct-form filter structures based on the difference equation. As a result, they can be very important for fixed-point implementations such as in custom VLSI or low-cost (fixed-point) signal processing chips. Lattice/ladder structures are also a good point of departure for computational physical models of acoustic systems such as vibrating strings, wind instrument bores, and the human vocal tract [81,16,48].

Next Section:
Testing Filter Stability in Matlab
Previous Section:
Computing Reflection Coefficients to Check Filter Stability