Symmetric Linear-Phase Filters
As stated at the beginning of this chapter, the impulse response of every causal, linear-phase, FIR filter is symmetric:
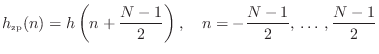

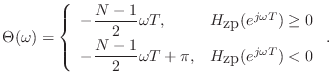
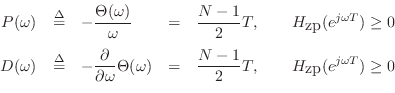
Simple Linear-Phase Filter Examples
- The example of §10.2.1 was in fact a linear-phase FIR
filter design example. The resulting causal finite impulse response
was left-shifted (``advanced'' in time) to make it zero phase.
- While the trivial ``bypass filter''
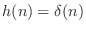 is zero-phase
(§10.2.2), the ``bypass filter with a unit delay,''
is zero-phase
(§10.2.2), the ``bypass filter with a unit delay,''
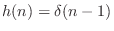 is linear phase. It is (trivially) symmetric
about time
is linear phase. It is (trivially) symmetric
about time 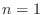 , and the frequency response is
, and the frequency response is
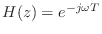 , which
is a pure linear phase term
, which
is a pure linear phase term
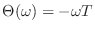 having a slope
of
having a slope
of 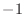 samples (radians per radians-per-sample), or
samples (radians per radians-per-sample), or 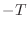 seconds
(radians per radians-per-second). The phase- and group-delays are
each 1 sample at every frequency.
seconds
(radians per radians-per-second). The phase- and group-delays are
each 1 sample at every frequency.
- The impulse response of the simplest lowpass filter studied in
Chapter 1 was
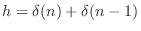 [
[
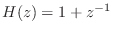 ].
Since this impulse response is symmetric about time
].
Since this impulse response is symmetric about time 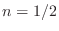 samples,
it is linear phase, and
samples,
it is linear phase, and
 , as derived
in Chapter 1. The phase delay and group delay are both
, as derived
in Chapter 1. The phase delay and group delay are both 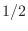 sample at
each frequency. Note that even-length linear-phase filters cannot be
time-shifted (without interpolation) to create a corresponding
zero-phase filter. However, they can be shifted to make a
near-zero-phase filter that has a phase delay and group delay equal to
half a sample at all passband frequencies.
sample at
each frequency. Note that even-length linear-phase filters cannot be
time-shifted (without interpolation) to create a corresponding
zero-phase filter. However, they can be shifted to make a
near-zero-phase filter that has a phase delay and group delay equal to
half a sample at all passband frequencies.
Software for Linear-Phase Filter Design
The Matlab Signal Processing Toolbox covers many applications with the following functions:
![$\displaystyle \begin{tabular}{rl}
\texttt{remez()} & (optimal Chebyshev linear-...
...or general FIR (or IIR)\\
& filter design \cite[page 50]{JOST}).
\end{tabular}$](http://www.dsprelated.com/josimages_new/filters/img1217.png)
Methods for FIR filter design are discussed in the fourth book of the music signal processing series [87], and classic references include [64,68]. There is also quite a large research literature on this subject.
Next Section:
Antisymmetric Linear-Phase Filters
Previous Section:
Odd Impulse Reponses




















