DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

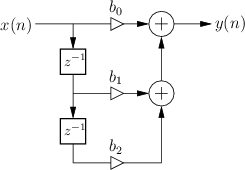
Two-Zero

The signal flow graph for the general two-zero filter is given in Fig.B.7, and the derivation of frequency response is as follows:

\fbox{ \begin{tabular}{rl} Difference equation: & $y(n) = b_0 x(n) + b_1 x(n-1) ... ...+ b_1 \cos(\omega T) + b_2 \cos(2\omega T)}\right]$ \end{tabular}\vspace{10pt} }

Figure B.7: Signal flow graph for the general two-zero filter
$ y(n) = b_0x(n) + b_1x(n - 1) + b_2x(n - 2)$.
\begin{figure}\input fig/twozero.pstex_t \end{figure}

As discussed in §5.1, the parameters $ b_1$ and $ b_2$ are called the numerator coefficients, and they determine the two zeros. Using the quadratic formula for finding the roots of a second-order polynomial, we find that the zeros are located at

$\displaystyle z = \frac{-b_1 \pm \sqrt{b_1^2 - 4 b_0 b_2}}{2b_0} $

If the zeros are real [ $ (b_1/2)^2 \geq b_2$], then the two-zero case reduces to two instances of our earlier analysis for the one-zero. Assuming the zeros to be complex, we may express the zeros in polar form as $ Re^{j\theta_c}$ and $ Re^{-j\theta_c}$, where $ \theta_c = \omega_c T = 2\pi f_c T$.

Forming a general two-zero transfer function in factored form gives

\begin{eqnarray*} H(z) &=& b_0 (1 - Re^{j\theta_c} z^{-1}) (1 - Re^{-j\theta_c} z^{-1})\\ &=& b_0 [1 - 2R\cos(\theta_c) z^{-1}+ R^2 z^{-2}] \end{eqnarray*}

from which we identify $ b_1/b_0 = - 2R \cos(\theta_c)$ and $ b_2/b_0 = R^2$, so that

$\displaystyle y(n) = b_0\{ x(n) - [2R \cos(\theta_c)]x(n - 1) + R^2 x(n - 2)\} $

is again the difference equation of the general two-zero filter with complex zeros. The frequency $ \omega$, is now viewed as a notch frequency, or antiresonance frequency. The closer R is to 1, the narrower the notch centered at $ \omega_c$.

The approximate relation between bandwidth and $ R$ given in Eq.$ \,$(B.5) for the two-pole resonator now applies to the notch width in the two-zero filter.

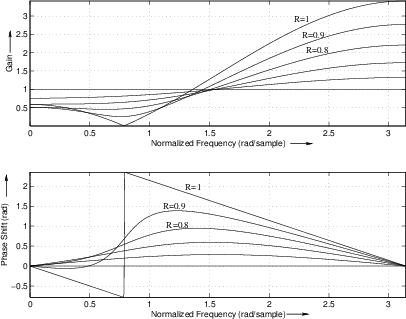
Figure B.8 gives some two-zero frequency responses obtained by setting $ b_0$ to 1 and varying $ R$. The value of $ \theta _c$, is again $ \pi /4$. Note that the response is exactly analogous to the two-pole resonator with notches replacing the resonant peaks. Since the plots are on a linear magnitude scale, the two-zero amplitude response appears as the reciprocal of a two-pole response. On a dB scale, the two-zero response is an upside-down two-pole response.

Figure B.8: Frequency response of the two-zero filter
$ y(n) = x(n) - 2R\cos (\theta _c) x(n - 1) + R^2 x(n - 2)$
with $ \theta _c$ fixed at $ \pi /4$ and for various values of $ R$. (a) Amplitude response. (b) Phase response.
\begin{figure}\input fig/kfig2p25.pstex_t \end{figure}

Next Section:
Complex Resonator
Previous Section:
Two-Pole