Free Books    Introduction to Digital Filters  

Two's Complement Wrap-Around

In this section, we give an example showing how temporary overflow in two's complement fixed-point causes no ill effects.

In 3-bit signed fixed-point arithmetic, the available numbers are as shown in Table 9.1.


Table 9.1: Three-bit two's-complement binary fixed-point numbers.
Decimal Binary
-4 100
-3 101
-2 110
-1 111
0 000
1 001
2 010
3 011


Let's perform the sum $ 3+3-4 = 2$, which gives a temporary overflow ($ 3+3=6$, which wraps around to $ -2$), but a final result ($ 2$) which is in the allowed range $ [-4,3]$:10.3

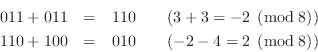
\begin{eqnarray*} 011 + 011 &=& 110 \qquad \mbox{$(3+3=-2\;\left(\mbox{mod}\;8\r... ...100 &=& 010 \qquad \mbox{$(-2-4=2\;\left(\mbox{mod}\;8\right))$} \end{eqnarray*}

Now let's do $ 1+3-2 = 2$ in three-bit two's complement:

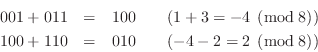
\begin{eqnarray*} 001 + 011 &=& 100 \qquad \mbox{$(1+3=-4\;\left(\mbox{mod}\;8\r... ...110 &=& 010 \qquad \mbox{$(-4-2=2\;\left(\mbox{mod}\;8\right))$} \end{eqnarray*}

In both examples, the intermediate result overflows, but the final result is correct. Another way to state what happened is that a positive wrap-around in the first addition is canceled by a negative wrap-around in the second addition.

Next Section:
More about Potential Internal Overflow of DF-II
Previous Section:
Derivation of Group Delay as Modulation Delay