Back to e
Above, we defined ![]() as the particular real number satisfying
as the particular real number satisfying
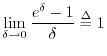
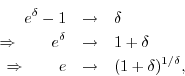
or
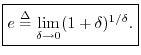
Numerically, ![]() is a transcendental number (a type of irrational
number3.5), so its decimal expansion never repeats.
The initial decimal expansion of
is a transcendental number (a type of irrational
number3.5), so its decimal expansion never repeats.
The initial decimal expansion of ![]() is given by3.6
is given by3.6
Next Section:
e^(j theta)
Previous Section:
Derivatives of f(x)=a^x




















