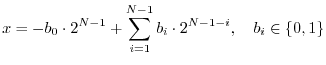Binary Integer Fixed-Point Numbers

Most computer languages nowadays only offer two kinds of numbers, floating-point and integer fixed-point. On present-day computers, all numbers are encoded using binary digits (called ``bits'') which are either 1 or 0.^G.1 In C, C++, and Java, floating-point variables are declared as float (32 bits) or double (64 bits), while integer fixed-point variables are declared as short int (typically 16 bits and never less), long int (typically 32 bits and never less), or simply int (typically the same as a long int, but sometimes between short and long). For an 8-bit integer, one can use the char data type (8 bits).

Since C was designed to accommodate a wide range of hardware, including old mini-computers, some latitude was historically allowed in the choice of these bit-lengths. The sizeof operator is officially the ``right way'' for a C program to determine the number of bytes in various data types at run-time, e.g., sizeof(long). (The word int can be omitted after short or long.) Nowadays, however, shorts are always 16 bits (at least on all the major platforms), ints are 32 bits, and longs are typically 32 bits on 32-bit computers and 64 bits on 64-bit computers (although some C/C++ compilers use long long int to declare 64-bit ints). Table G.1 gives the lengths currently used by GNU C/C++ compilers (usually called ``gcc'' or ``cc'') on 64-bit processors.^G.2

Type	Bytes	Notes
`char`	1
`short`	2
`int`	4
`long`	8	(4 bytes on 32-bit machines)
`long long`	8	(may become 16 bytes)
`type *`	8	(any pointer)
`float`	4
`double`	8
`long double`	8	(may become 10 bytes)
`size_t`	8	(type of sizeof())
T* - T*	8	(pointer arithmetic)

Java, which is designed to be platform independent, defines a long int as equivalent in precision to 64 bits, an int as 32 bits, a short int as 16 bits, and additionally a byte int as an 8-bit int. Similarly, the ``Structured Audio Orchestra Language'' (SAOL) (pronounced ``sail'')--the sound-synthesis component of the new MPEG-4 audio compression standard--requires only that the underlying number system be at least as accurate as 32-bit floats. All ints discussed thus far are signed integer formats. C and C++ also support unsigned versions of all int types, and they range from 0 to

instead of $-2^{N-1}$ to $2^{N-1}-1$ , where

is the number of bits. Finally, an unsigned char is often used for integers that only range between 0 and 255.

One's Complement Fixed-Point Format

One's Complement is a particular assignment of bit patterns to numbers. For example, in the case of 3-bit binary numbers, we have the assignments shown in Table G.2.

Table G.2: Three-bit one's-complement binary fixed-point numbers.

Binary	Decimal
000	0
001	1
010	2
011	3
100	-3
101	-2
110	-1
111	-0

In general,

-bit numbers are assigned to binary counter values in the ``obvious way'' as integers from 0 to $2^{N-1}-1$ , and then the negative numbers are assigned in reverse order, as shown in the example. The term ``one's complement'' refers to the fact that negating a number in this format is accomplished by simply complementing the bit pattern (inverting each bit). Note that there are two representations for zero (all 0s and all 1s). This is inconvenient when testing if a number is equal to zero. For this reason, one's complement is generally not used.

Two's Complement Fixed-Point Format

In two's complement, numbers are negated by complementing the bit pattern and adding 1, with overflow ignored. From 0 to $2^{N-1}-1$ , positive numbers are assigned to binary values exactly as in one's complement. The remaining assignments (for the negative numbers) can be carried out using the two's complement negation rule. Regenerating the

example in this way gives Table G.3.

Table G.3: Three-bit two's-complement binary fixed-point numbers.

Binary	Decimal
000	0
001	1
010	2
011	3
100	-4
101	-3
110	-2
111	-1

Note that according to our negation rule,

. Logically, what has happened is that the result has ``overflowed'' and ``wrapped around'' back to itself. Note that

also. In other words, if you compute 4 somehow, since there is no bit-pattern assigned to 4, you get -4, because -4 is assigned the bit pattern that would be assigned to 4 if

were larger. Note that numerical overflows naturally result in ``wrap around'' from positive to negative numbers (or from negative numbers to positive numbers). Computers normally ``trap'' overflows as an ``exception.'' The exceptions are usually handled by a software ``interrupt handler,'' and this can greatly slow down the processing by the computer (one numerical calculation is being replaced by a rather sizable program). Note that temporary overflows are ok in two's complement; that is, if you add

to get

, adding

will give

again. This is why two's complement is a nice choice: it can be thought of as placing all the numbers on a ``ring,'' allowing temporary overflows of intermediate results in a long string of additions and/or subtractions. All that matters is that the final sum lie within the supported dynamic range. Computers designed with signal processing in mind (such as so-called ``Digital Signal Processing (DSP) chips'') generally just do the best they can without generating exceptions. For example, overflows quietly ``saturate'' instead of ``wrapping around'' (the hardware simply replaces the overflow result with the maximum positive or negative number, as appropriate, and goes on). Since the programmer may wish to know that an overflow has occurred, the first occurrence may set an ``overflow indication'' bit which can be manually cleared. The overflow bit in this case just says an overflow happened sometime since it was last checked.

Two's-Complement, Integer Fixed-Point Numbers

Let

denote the number of bits. Then the value of a two's complement integer fixed-point number can be expressed in terms of its bits $\{b_i\}_{i=0}^{N-1}$ as

$\displaystyle x = - b_0 \cdot 2^{N-1} + \sum_{i=1}^{N - 1} b_i \cdot 2^{N - 1 - i},\quad b_i\in\{0,1\} \protect$

(G.1)

We visualize the binary word containing these bits as

$\displaystyle x = [b_0\, b_1\, \cdots\, b_{N-1}]$

Each bit

is of course either 0 or 1. Check that the

case in Table G.3 is computed correctly using this formula. As an example, the number 3 is expressed as

$\displaystyle 3 =[ 0 1 1 ] = - 0\cdot 4 + 1\cdot 2 + 1 \cdot 1$

while the number -3 is expressed as

$\displaystyle -3 =[ 1 0 1 ] = - 1\cdot 4 + 0\cdot 2 + 1 \cdot 1$

and so on. The most-significant bit in the word,

, can be interpreted as the ``sign bit''. If

is ``on'', the number is negative. If it is ``off'', the number is either zero or positive. The least-significant bit is $b_{N-1}$ . ``Turning on'' that bit adds 1 to the number, and there are no fractions allowed. The largest positive number is when all bits are on except