Geometric Signal Theory
This section follows Chapter 5 of the text.
Vector Interpretation of Complex Numbers
Here's how Fig.5.1 may be generated in matlab:
>> x = [2 3]; % coordinates of x >> origin = [0 0]; % coordinates of the origin >> xcoords = [origin(1) x(1)]; % plot() expects coordinates >> ycoords = [origin(2) x(2)]; >> plot(xcoords,ycoords); % Draw a line from origin to x
Signal Metrics
The mean of a signal ![]() stored in a matlab row- or column-vector
x can be computed in matlab as
stored in a matlab row- or column-vector
x can be computed in matlab as
mu = sum(x)/Nor by using the built-in function mean(). If x is a 2D matrix containing N elements, then we need mu = sum(sum(x))/N or mu = mean(mean(x)), since sum computes a sum along ``dimension 1'' (which is along columns for matrices), and mean is implemented in terms of sum. For 3D matrices, mu = mean(mean(mean(x))), etc. For a higher dimensional matrices x, ``flattening'' it into a long column-vector x(:) is the more concise form:
N = prod(size(x)) mu = sum(x(:))/Nor
mu = x(:).' * ones(N,1)/NThe above constructs work whether x is a row-vector, column-vector, or matrix, because x(:) returns a concatenation of all columns of x into one long column-vector. Note the use of .' to obtain non-conjugating vector transposition in the second form. N = prod(size(x)) is the number of elements of x. If x is a row- or column-vector, then length(x) gives the number of elements. For matrices, length() returns the greater of the number of rows or columns.I.1
Signal Energy and Power
In a similar way, we can compute the signal energy
![]() (sum of squared moduli) using any of the following constructs:
(sum of squared moduli) using any of the following constructs:
Ex = x(:)' * x(:) Ex = sum(conj(x(:)) .* x(:)) Ex = sum(abs(x(:)).^2)The average power (energy per sample) is similarly Px = Ex/N. The
Inner Product
The inner product
![]() of two column-vectors x and
y (§5.9)
is conveniently computed in matlab as
of two column-vectors x and
y (§5.9)
is conveniently computed in matlab as
xdoty = y' * x
Vector Cosine
For real vectors x and y having the same length, we may compute the vector cosine by
cosxy = y' * x / ( norm(x) * norm(y) );For complex vectors, a good measure of orthogonality is the modulus of the vector cosine:
collinearity = abs(y' * x) / ( norm(x) * norm(y) );Thus, when collinearity is near 0, the vectors x and y are substantially orthogonal. When collinearity is close to 1, they are nearly collinear.
Projection
As discussed in §5.9.9,
the orthogonal projection of
![]() onto
onto
![]() is defined by
is defined by
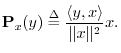
yx = (x' * y) * (x' * x)^(-1) * xMore generally, a length-N column-vector y can be projected onto the
yX = X * (X' * X)^(-1) * X' * yOrthogonal projection, like any finite-dimensional linear operator, can be represented by a matrix. In this case, the
PX = X * (X' * X)^(-1) * X'is called the projection matrix.I.2Subspace projection is an example in which the power of matrix linear algebra notation is evident.
Projection Example 1
>> X = [[1;2;3],[1;0;1]] X = 1 1 2 0 3 1 >> PX = X * (X' * X)^(-1) * X' PX = 0.66667 -0.33333 0.33333 -0.33333 0.66667 0.33333 0.33333 0.33333 0.66667 >> y = [2;4;6] y = 2 4 6 >> yX = PX * y yX = 2.0000 4.0000 6.0000
Since y in this example already lies in the column-space of X, orthogonal projection onto that space has no effect.
Projection Example 2
Let X and PX be defined as Example 1, but now let
>> y = [1;-1;1] y = 1 -1 1 >> yX = PX * y yX = 1.33333 -0.66667 0.66667 >> yX' * (y-yX) ans = -7.0316e-16 >> eps ans = 2.2204e-16
In the last step above, we verified that the projection yX is
orthogonal to the ``projection error'' y-yX, at least to
machine precision. The eps variable holds ``machine
epsilon'' which is the numerical distance
between ![]() and the next representable number in double-precision
floating point.
and the next representable number in double-precision
floating point.
Orthogonal Basis Computation
Matlab and Octave have a function orth() which will compute an orthonormal basis for a space given any set of vectors which span the space. In Matlab, e.g., we have the following help info:
>> help orth
ORTH Orthogonalization.
Q = orth(A) is an orthonormal basis for the range of A.
Q'*Q = I, the columns of Q span the same space as the
columns of A and the number of columns of Q is the rank
of A.
See also QR, NULL.
Below is an example of using orth() to orthonormalize a linearly
independent basis set for ![]() :
:
% Demonstration of the orth() function. v1 = [1; 2; 3]; % our first basis vector (a column vector) v2 = [1; -2; 3]; % a second, linearly independent vector v1' * v2 % show that v1 is not orthogonal to v2 ans = 6 V = [v1,v2] % Each column of V is one of our vectors V = 1 1 2 -2 3 3 W = orth(V) % Find an orthonormal basis for the same space W = 0.2673 0.1690 0.5345 -0.8452 0.8018 0.5071 w1 = W(:,1) % Break out the returned vectors w1 = 0.2673 0.5345 0.8018 w2 = W(:,2) w2 = 0.1690 -0.8452 0.5071 w1' * w2 % Check that w1 is orthogonal to w2 ans = 2.5723e-17 w1' * w1 % Also check that the new vectors are unit length ans = 1 w2' * w2 ans = 1 W' * W % faster way to do the above checks ans = 1 0 0 1 % Construct some vector x in the space spanned by v1 and v2: x = 2 * v1 - 3 * v2 x = -1 10 -3 % Show that x is also some linear combination of w1 and w2: c1 = x' * w1 % Coefficient of projection of x onto w1 c1 = 2.6726 c2 = x' * w2 % Coefficient of projection of x onto w2 c2 = -10.1419 xw = c1 * w1 + c2 * w2 % Can we make x using w1 and w2? xw = -1 10 -3 error = x - xw error = 1.0e-14 * 0.1332 0 0 norm(error) % typical way to summarize a vector error ans = 1.3323e-15 % It works! (to working precision, of course)
% Construct a vector x NOT in the space spanned by v1 and v2: y = [1; 0; 0]; % Almost anything we guess in 3D will work % Try to express y as a linear combination of w1 and w2: c1 = y' * w1; % Coefficient of projection of y onto w1 c2 = y' * w2; % Coefficient of projection of y onto w2 yw = c1 * w1 + c2 * w2 % Can we make y using w1 and w2?
yw =
0.1
0.0
0.3
yerror = y - yw
yerror =
0.9
0.0
-0.3
norm(yerror)
ans =
0.9487
While the error is not zero, it is the smallest possible error in the
least squares sense. That is, yw is the optimal
least-squares approximation to y in the space spanned by v1
and v2 (w1 and w2). In other words,
norm(yerror) is less than or equal to norm(y-yw2) for any
other vector yw2 made using a linear combination of
v1 and v2. In yet other words, we obtain the
optimal least squares approximation of
y (which lives in 3D) in some subspace ![]() (a 2D subspace of 3D
spanned by the columns of matrix W) by projecting
y orthogonally onto the subspace
(a 2D subspace of 3D
spanned by the columns of matrix W) by projecting
y orthogonally onto the subspace ![]() to get
yw as above.
to get
yw as above.
An important property of the optimal least-squares approximation is that the approximation error is orthogonal to the the subspace in which the approximation lies. Let's verify this:
W' * yerror % must be zero to working precision ans = 1.0e-16 * -0.2574 -0.0119
Next Section:
The DFT
Previous Section:
Factoring Polynomials in Matlab




















