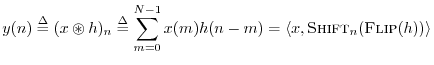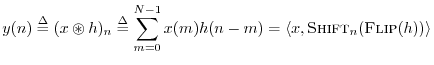Free Books
   Free Books    Mathematics of the DFT  

Graphical Convolution

As mentioned above, cyclic convolution can be written as

$\displaystyle y(n) \isdef (x\circledast h)_n \isdef \sum_{m=0}^{N-1}x(m)h(n-m) = \left<x,\hbox{\sc Shift}_n(\hbox{\sc Flip}(h))\right>$   $\displaystyle \mbox{($h$\ real)}$

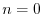
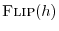
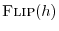
where $ x,y\in{\bf C}^N$ and $ h\in{\bf R}^N$. It is instructive to interpret this expression graphically, as depicted in Fig.7.5 above. The convolution result at time $ n=0$ is the inner product of $ x$ and $ \hbox{\sc Flip}(h)$, or $ y(0)=\left<x,\hbox{\sc Flip}(h)\right>$. For the next time instant, $ n=1$, we shift $ \hbox{\sc Flip}(h)$ one sample to the right and repeat the inner product operation to obtain $ y(1)=\left<x,\hbox{\sc Shift}_1(\hbox{\sc Flip}(h))\right>$, and so on. 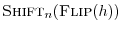To capture the cyclic nature of the convolution, $ x$ and $ \hbox{\sc Shift}_n(\hbox{\sc Flip}(h))$ can be imagined plotted on a cylinder. 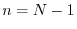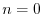Thus, Fig.7.5 shows the cylinder after being ``cut'' along the vertical line between $ n=N-1$ and $ n=0$ and ``unrolled'' to lay flat.

Next Section:
Polynomial Multiplication
Previous Section:
Convolution Example 3: Matched Filtering