DSPRelated.com
Free Books
   Free Books    Mathematics of the DFT  

Informal Derivation of Taylor Series

We have a function $ f(x)$ and we want to approximate it using an $ n$th-order polynomial:

$\displaystyle f(x) = f_0 + f_1 x + f_2 x^2 + \cdots + f_n x^n + R_{n+1}(x) $

where $ R_{n+1}(x)$, the approximation error, is called the remainder term. We may assume $ x$ and $ f(x)$ are real, but the following derivation generalizes unchanged to the complex case.

Our problem is to find fixed constants $ \{f_i\}_{i=0}^{n}$ so as to obtain the best approximation possible. Let's proceed optimistically as though the approximation will be perfect, and assume $ R_{n+1}(x)=0$ for all $ x$ ( $ R_{n+1}(x)\equiv0$), given the right values of $ f_i$. Then at $ x=0$ we must have

$\displaystyle f(0) = f_0 $

That's one constant down and $ n-1$ to go! Now let's look at the first derivative of $ f(x)$ with respect to $ x$, again assuming that $ R_{n+1}(x)\equiv0$:

$\displaystyle f^\prime(x) = 0 + f_1 + 2 f_2 x + 3 f_2 x^2 + \cdots + n f_n x^{n-1} $

Evaluating this at $ x=0$ gives

$\displaystyle f^\prime(0) = f_1. $

In the same way, we find

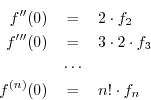
\begin{eqnarray*} f^{\prime\prime}(0) &=& 2 \cdot f_2 \\ f^{\prime\prime\prime}... ...cdot 2 \cdot f_3 \\ & \cdots & \\ f^{(n)}(0) &=& n! \cdot f_n \end{eqnarray*}

where $ f^{(n)}(0)$ denotes the $ n$th derivative of $ f(x)$ with respect to $ x$, evaluated at $ x=0$. Solving the above relations for the desired constants yields

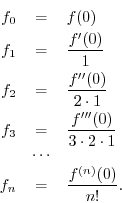
\begin{eqnarray*} f_0 &=& f(0) \\ f_1 &=& \frac{f^{\prime}(0)}{1} \\ f_2 &=& \... ...dot 2\cdot 1} \\ & \cdots & \\ f_n &=& \frac{f^{(n)}(0)}{n!}. \end{eqnarray*}

Thus, defining $ 0!\isdef 1$ (as it always is), we have derived the following polynomial approximation:

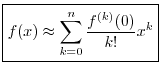
$\displaystyle \zbox {f(x) \approx \sum_{k=0}^n \frac{f^{(k)}(0)}{k!} x^k} $

This is the $ n$th-order Taylor series expansion of $ f(x)$ about the point $ x=0$. Its derivation was quite simple. The hard part is showing that the approximation error (remainder term $ R_{n+1}(x)$) is small over a wide interval of $ x$ values. Another ``math job'' is to determine the conditions under which the approximation error approaches zero for all $ x$ as the order $ n$ goes to infinity. The main point to note here is that the Taylor series itself is simple to derive.

Next Section:
Taylor Series with Remainder
Previous Section:
Appendix: Frequencies Representable by a Geometric Sequence