DSPRelated.com
Free Books
   Free Books    Mathematics of the DFT  

Linear Vector Space

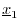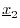A set of vectors may be called a linear vector space if it is closed under linear combinations. That is, given any two vectors $ \underline{x}_1$ and $ \underline{x}_2$ from the set, the linear combination

$\displaystyle \underline{y}= \alpha_1\underline{x}_1 + \alpha_2\underline{x}_2 $

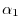
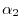
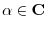
is also in the set, for all scalars $ \alpha_1$ and $ \alpha_2$. In our context, most generally, the vector coordinates and the scalars can be any complex numbers. Since complex numbers are closed under multiplication and addition, it follows that the set of all vectors in $ {\bf C}^N$ with complex scalars ( $ \alpha\in{\bf C}$) forms a linear vector space. 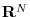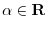The same can be said of real length-$ N$ vectors in $ {\bf R}^N$ with real scalars ( $ \alpha\in{\bf R}$). However, real vectors with complex scalars do not form a vector space, since scalar multiplication can take a real vector to a complex vector outside of the set of real vectors.

Next Section:
Signal Metrics
Previous Section:
Linear Combination of Vectors