Free Books
   Free Books    Mathematics of the DFT  

Linearity of the Inner Product

Any function $ f(\underline{u})$ of a vector $ \underline{u}\in{\bf C}^N$ (which we may call an operator on $ {\bf C}^N$) is said to be linear if for all $ \underline{u}\in{\bf C}^N$ and $ \underline{v}\in{\bf C}^N$, and for all scalars $ \alpha$ and $ \beta $ in $ {\bf C}$,

$\displaystyle f(\alpha \underline{u}+ \beta \underline{v}) = \alpha f(\underline{u}) + \beta f(\underline{v}). $

A linear operator thus ``commutes with mixing.'' Linearity consists of two component properties:
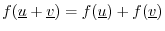
  • additivity: $ f(\underline{u}+\underline{v}) = f(\underline{u}) + f(\underline{v})$
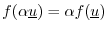
  • homogeneity: $ f(\alpha \underline{u}) = \alpha f(\underline{u})$
A function of multiple vectors, e.g., $ f(\underline{u},\underline{v},\underline{w})$ can be linear or not with respect to each of its arguments.

The inner product $ \left<\underline{u},\underline{v}\right>$ is linear in its first argument, i.e., for all $ \underline{u},\underline{v},\underline{w}\in{\bf C}^N$, and for all $ \alpha, \beta\in{\bf C}^N$,

$\displaystyle \left<\alpha \underline{u}+ \beta \underline{v},\underline{w}\rig... ...line{u},\underline{w}\right> + \beta \left<\underline{v},\underline{w}\right>. $

This is easy to show from the definition:

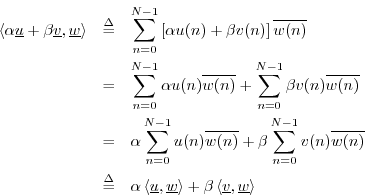
\begin{eqnarray*} \left<\alpha \underline{u}+ \beta \underline{v},\underline{w}\... ...rline{w}\right> + \beta \left<\underline{v},\underline{w}\right> \end{eqnarray*}

The inner product is also additive in its second argument, i.e.,

$\displaystyle \left<\underline{u},\underline{v}+ \underline{w}\right> = \left<\underline{u},\underline{v}\right> + \left<\underline{u},\underline{w}\right>, $

but it is only conjugate homogeneous (or antilinear) in its second argument, since

$\displaystyle \left<\underline{u},\alpha \underline{v}\right> = \overline{\alph... ...{u},\underline{v}\right> \neq \alpha \left<\underline{u},\underline{v}\right>. $

The inner product is strictly linear in its second argument with respect to real scalars $ a$ and $ b$:

$\displaystyle \left<\underline{u},a \underline{v}+ b \underline{w}\right> = a \... ...ne{v}\right> + b \left<\underline{u},\underline{w}\right>, \quad a,b\in{\bf R} $

where $ \underline{u},\underline{v},\underline{w}\in{\bf C}^N$.

Since the inner product is linear in both of its arguments for real scalars, it may be called a bilinear operator in that context.

Next Section:
Norm Induced by the Inner Product
Previous Section:
Banach Spaces