Free Books    Mathematics of the DFT  

Matched Filtering

The cross-correlation function is used extensively in pattern recognition and signal detection. We know from Chapter 5 that projecting one signal onto another is a means of measuring how much of the second signal is present in the first. This can be used to ``detect'' the presence of known signals as components of more complicated signals. As a simple example, suppose we record $ x(n)$ which we think consists of a signal $ s(n)$ that we are looking for plus some additive measurement noise $ e(n)$. That is, we assume the signal model $ x(n)=s(n)+e(n)$. Then the projection of $ x$ onto $ s$ is (recalling §5.9.9)

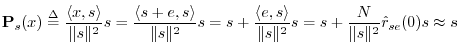
$\displaystyle {\bf P}_s(x) \isdef \frac{\left<x,s\right>}{\Vert s\Vert^2} s = \... ...}{\Vert s\Vert^2} s = s + \frac{N}{\Vert s\Vert^2} {\hat r}_{se}(0)s \approx s $

since the projection of random, zero-mean noise $ e$ onto $ s$ is small with probability one. Another term for this process is matched filtering. The impulse response of the ``matched filter'' for a real signal $ s$ is given by $ \hbox{\sc Flip}(s)$.8.11 By time-reversing $ s$, we transform the convolution implemented by filtering into a sliding cross-correlation operation between the input signal $ x$ and the sought signal $ s$. (For complex known signals $ s$, the matched filter is $ \hbox{\sc Flip}(\overline{s})$.) We detect occurrences of $ s$ in $ x$ by detecting peaks in $ {\hat r}_{sx}(l)$.

In the same way that FFT convolution is faster than direct convolution (see Table 7.1), cross-correlation and matched filtering are generally carried out most efficiently using an FFT algorithm (Appendix A).

Next Section:
FIR System Identification
Previous Section:
Autocorrelation