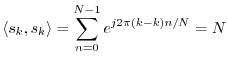Norm of the DFT Sinusoids
For ![]() , we follow the previous derivation to the next-to-last step to get
, we follow the previous derivation to the next-to-last step to get
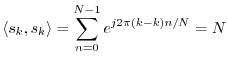
Next Section:
An Orthonormal Sinusoidal Set
Previous Section:
Orthogonality of the DFT Sinusoids
For ![]() , we follow the previous derivation to the next-to-last step to get
, we follow the previous derivation to the next-to-last step to get