Norm Properties
There are many other possible choices of norm. To qualify as a norm
on  , a real-valued signal-function
, a real-valued signal-function
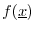 must
satisfy the following three properties:
must
satisfy the following three properties:
-
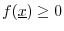 , with
, with
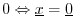
-
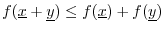
-
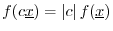 ,
,

The first property, ``positivity,'' says the norm is nonnegative, and
only the zero vector has norm zero. The second property is
``subadditivity'' and is sometimes called the ``
triangle inequality''
for reasons that can be seen by studying
Fig.
5.6. The third property says the norm is
``absolutely homogeneous'' with respect to
scalar multiplication. (The
scalar 
can be complex, in which case the angle of

has no effect).
Next Section: Banach SpacesPrevious Section: Other Lp Norms
![]() , a real-valued signal-function
, a real-valued signal-function
![]() must
satisfy the following three properties:
must
satisfy the following three properties:
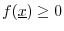 , with
, with
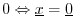
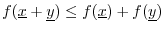
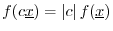 ,
,





















