DSPRelated.com
Free Books
   Free Books    Mathematics of the DFT  


Preface

The Discrete Fourier Transform (DFT) can be understood as a numerical approximation to the Fourier transform. However, the DFT has its own exact Fourier theory, which is the main focus of this book. The DFT is normally encountered in practice as a Fast Fourier Transform (FFT)--i.e., a high-speed algorithm for computing the DFT. FFTs are used extensively in a wide range of digital signal processing applications, including spectrum analysis, high-speed convolution (linear filtering), filter banks, signal detection and estimation, system identification, audio compression (e.g., MPEG-II AAC), spectral modeling sound synthesis, and many other applications; some of these will be discussed in Chapter 8.

This book started out as a series of readers for my introductory course in digital audio signal processing that I have given at the Center for Computer Research in Music and Acoustics (CCRMA) since 1984. The course was created primarily for entering Music Ph.D. students in the Computer Based Music Theory program at CCRMA. As a result, the only prerequisite is a good high-school math background, including some calculus exposure.

Chapter Outline

  1. ``Introduction to the DFT'' points out the mathematical elements which will be discussed in this book, all motivated by the DFT.

  2. ``Introduction to Complex Numbers'' is about factoring polynomials, the quadratic formula, the complex plane, and Euler's formula.

  3. ``Proof of Euler's Identity'' derives Euler's identity in detail. This is an important tool for working with complex numbers, and one of the critical elements of the DFT definition we need to understand.

  4. ``Sinusoids and Exponentials'' is devoted to two of the most elementary signals in signal processing--sinusoids and exponentials. Also covered are complex sinusoids, audio decay time ($ t_{60}$), in-phase and quadrature sinusoidal components, analytic signals, positive and negative frequencies, constructive and destructive interference, invariance of sinusoidal frequency in linear time-invariant systems, circular motion as the vector sum of in-phase and quadrature sinusoidal motions, sampled sinusoids, and generating sampled sinusoids from powers of a unit-modulus complex number.

  5. ``Geometric Signal Theory'' provides an introduction to vector spaces, inner products, orthogonality, projection of one signal onto another, norms, and elementary vector space operations. In this setting, the DFT can be regarded as a change of coordinates from one basis set (shifted impulses) to another (sinusoids at different frequencies).

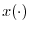  6. ``The DFT Derived'' derives the DFT as a projection of a length $ N$ signal $ x(\cdot)$ onto the set of $ N$ sampled complex sinusoids generated by the $ N$th roots of unity.

  7. ``Fourier Theorems for the DFT'' derives basic Fourier symmetry relations, the shift theorem, convolution theorem, correlation theorem, power theorem, and theorems pertaining to interpolation and downsampling.

  8. ``Example Applications of the DFT'' illustrates practical FFT analysis in Matlab $ ^{\hbox{\scriptsize\textcircled{\tiny R}}}$ and Octave (an open-source matlab) through a series of examples. The various Fourier theorems of the preceding chapter provide a ``thinking vocabulary'' for understanding these applications.

Elementary and supporting information is provided in a series of appendices. Topics include introductions to sampling theory, Taylor series expansions, logarithms, decibels, digital audio number systems, matrices, round-off noise, Fourier series, and continuous-time Fourier theorems, such as the similarity and differentiation theorems. As a segue to computer-based approaches, a well used Fast Fourier Transform (FFT) algorithm is derived. Finally, various software examples in the Matlab (or Octave) programming language are presented.

This book is first in a series of course readers for my signal processing courses at CCRMA:

  1. Mathematics of the Discrete Fourier Transform (DFT):
    http://www.dsprelated.com/dspbooks/mdft/
  2. Introduction to Digital Filters:
    http://www.dsprelated.com/dspbooks/filters/
  3. Physical Audio Signal Processing
    (the ``physical modeling book''):
    http://www.dsprelated.com/dspbooks/pasp/
  4. Spectral Audio Signal Processing
    (the ``spectral modeling book''):
    http://www.dsprelated.com/dspbooks/sasp/
  5. Audio Digital Filter Design
    (an update of Chapter 1 of my PhD/EE thesis [66]):
    http://ccrma.stanford.edu/~jos/adfd/

Acknowledgments

Thanks to my graduate students and research colleagues Sean Bratnober, Mark Cartwright, Humane Chan, Rob Hamilton, Miriam Kolar, Randal Leistikow, Sandy Lin, Gautham Mysore, Juhan Nam, Jeonghun Noh, Brook Reeder, Bill Schottstaedt, Sook Young Won, Vivian Woo, and Matt Wright for helpful errata reporting and other suggestions based on earlier precursors to this book. Special thanks are due to Miller Puckette for some especially useful contributions. Thanks also to netizens Greg Allen, Adi Biton, John Brenneise, David Holman, Alexander Kraus, Nima Maftoon, Niels Moseley, Hirak Parikh, and Eric Woudenberg for reporting errata in the draft versions on the Web. Additionally, email discussions with Steven Johnson (co-author of the well known FFTW software package) contributed greatly to the appendix on FFT algorithms.

Many thanks to my 1997 teaching assistant Craig Stuart Sapp for writing the Mathematica magic for Figures 4.9 (adapted for the cover), 4.17, 4.18, 4.19, 7.5, 7.9, 7.11, and 7.12.

Thanks also to Prof. C. Sidney Burrus of Rice University for teaching me and others the fundamentals of digital signal processing, including the DFT.

Finally, thanks to my wife Carol for her encouragement and support, and for putting up with all those ``working Saturdays'', and to my son Harrison, age 9, for his many inspirations, both musical and mathematical, among others.


Julius Smith
April, 2007

Errata

While I have tried, with help from my students and interested colleagues, to compose a correct manuscript, it is inevitable that ``suboptimalities'' will be discovered over time. The Web page http://books.w3k.org/mdft2/ will list any known errata, clarifications, or other information pertaining to this book.

The author and publisher make no warranties, express or implied, regarding the contents of this book.

Next Section:
Introduction to the DFT