Projection onto Non-Orthogonal Vectors

Consider this example:

$\begin{eqnarray*} \sv_0 &\isdef & [1,1] \\ \sv_1 &\isdef & [0,1] \end{eqnarray*}$

These point in different directions, but they are not orthogonal. What happens now? The projections are

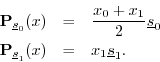
$\begin{eqnarray*} {\bf P}_{\sv_0}(x) &=& \frac{x_0 + x_1}{2}\sv_0 \\ {\bf P}_{\sv_1}(x) &=& x_1\sv_1. \end{eqnarray*}$

The sum of the projections is

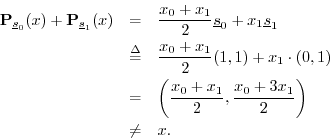
$\begin{eqnarray*} {\bf P}_{\sv_0}(x) + {\bf P}_{\sv_1}(x) &=& \frac{x_0 + x_1}... ...\frac{x_0 + x_1}{2}, \frac{x_0 + 3x_1}{2}\right) \\ &\neq& x. \end{eqnarray*}$

So, even though the vectors are linearly independent, the sum of projections onto them does not reconstruct the original vector. Since the sum of projections worked in the orthogonal case, and since orthogonality implies linear independence, we might conjecture at this point that the sum of projections onto a set of vectors will reconstruct the original vector only when the vector set is orthogonal, and this is true, as we will show.

It turns out that one can apply an orthogonalizing process, called Gram-Schmidt orthogonalization to any linearly independent vectors in ${\bf C}^N$ so as to form an orthogonal set which will always work. This will be derived in Section 5.10.4.

Obviously, there must be at least vectors in the set. Otherwise, there would be too few degrees of freedom to represent an arbitrary $x\in{\bf C}^N$ . That is, given the coordinates $\{u(n)\}_{n=0}^{N-1}$ of (which are scale factors relative to the coordinate vectors $\underline{e}_n$ in ${\bf C}^N$ ), we have to find at least coefficients of projection (which we may think of as coordinates relative to new coordinate vectors $\sv_k$ ). If we compute only coefficients, then we would be mapping a set of complex numbers to numbers. Such a mapping cannot be invertible in general. It also turns out linearly independent vectors is always sufficient. The next section will summarize the general results along these lines.