Free Books
   Free Books    Mathematics of the DFT  

Triangle Difference Inequality

A useful variation on the triangle inequality is that the length of any side of a triangle is greater than the absolute difference of the lengths of the other two sides:

$\displaystyle \zbox {\Vert\underline{u}-\underline{v}\Vert \geq \left\vert\Vert\underline{u}\Vert - \Vert\underline{v}\Vert\right\vert} $


Proof: By the triangle inequality,

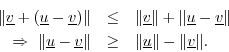
\begin{eqnarray*} \Vert\underline{v}+ (\underline{u}-\underline{v})\Vert &\leq &... ...}\Vert &\geq& \Vert\underline{u}\Vert - \Vert\underline{v}\Vert. \end{eqnarray*}

Interchanging $ \underline{u}$ and $ \underline{v}$ establishes the absolute value on the right-hand side.

Next Section:
Vector Cosine
Previous Section:
Triangle Inequality