DSPRelated.com
Free Books
   Free Books    Mathematics of the DFT  

Triangle Inequality

The triangle inequality states that the length of any side of a triangle is less than or equal to the sum of the lengths of the other two sides, with equality occurring only when the triangle degenerates to a line. In $ {\bf C}^N$, this becomes

$\displaystyle \zbox {\Vert\underline{u}+\underline{v}\Vert \leq \Vert\underline{u}\Vert + \Vert\underline{v}\Vert.} $

We can show this quickly using the Schwarz Inequality:

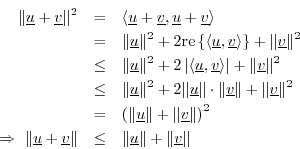
\begin{eqnarray*} \Vert\underline{u}+\underline{v}\Vert^2 &=& \left<\underline{u... ...v}\Vert &\leq& \Vert\underline{u}\Vert + \Vert\underline{v}\Vert \end{eqnarray*}

Next Section:
Triangle Difference Inequality
Previous Section:
Cauchy-Schwarz Inequality