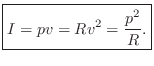Acoustic Intensity
Acoustic intensity may be defined by
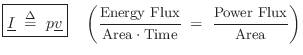
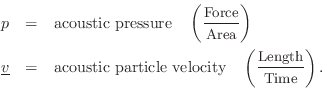
For a plane traveling wave, we have
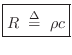
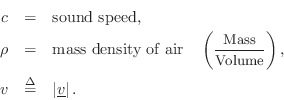
Therefore, in a plane wave,
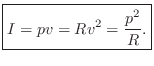
Next Section:
Acoustic Energy Density
Previous Section:
Air Jets
Acoustic intensity may be defined by
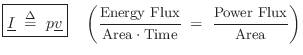
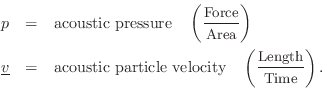
For a plane traveling wave, we have
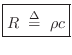
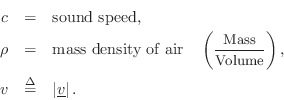
Therefore, in a plane wave,