The relative amount of compression/expansion energy that goes into
temperature  versus pressure
versus pressure 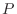 can be characterized by the heat capacity ratio
can be characterized by the heat capacity ratio
where
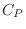
is the
specific heat (also called
heat
capacity) at constant pressure, while

is the specific heat at
constant volume. The
specific heat, in turn, is the amount of
heat required to raise the temperature of the gas by one degree. It
is derived in
statistical thermodynamics [
138]
that, for an
ideal gas, we have
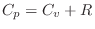
, where

is the
ideal
gas constant (introduced in Eq.

(
B.45)). Thus,
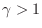
for any
ideal gas. The extra heat absorption that occurs when heating a gas
at constant pressure is associated with the
work (§
B.2)
performed on the volume boundary (fore times distance = pressure times
area times distance) as it expands to keep pressure constant. Heating
a gas at constant volume involves increasing the
kinetic energy of the
molecules, while heating a gas at constant pressure involves both that
and pushing the boundary of the volume out. The reason not all
gases have the same
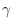
is that they have different
internal degrees of freedom, such as those associated with
spinning and vibrating internally. Each degree of freedom can store
energy.
In terms of 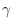 , we have
, we have
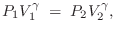 |
(B.46) |
where
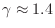
for dry air at normal temperatures. Thus,
if a volume of ideal gas is changed from
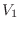
to
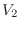
, the pressure
change is given by
and the temperature change is
These equations both follow from Eq.

(
B.46) and the
ideal gas law
Eq.

(
B.45).
The value
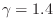 is typical for any diatomic
gas.B.31 Monatomic inert gases, on the other hand,
such as Helium, Neon, and Argon, have
is typical for any diatomic
gas.B.31 Monatomic inert gases, on the other hand,
such as Helium, Neon, and Argon, have
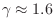 . Carbon
dioxide, which is triatomic, has a heat capacity ratio
. Carbon
dioxide, which is triatomic, has a heat capacity ratio
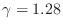 . We see that more complex molecules have lower
. We see that more complex molecules have lower 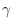 values because they can store heat in more degrees of freedom.
values because they can store heat in more degrees of freedom.
Next Section: Heat Capacity of Ideal GasesPrevious Section: Isothermal versus Isentropic
![]() versus pressure
versus pressure ![]() can be characterized by the heat capacity ratio
can be characterized by the heat capacity ratio
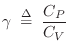
![]() , we have
, we have
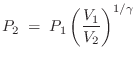
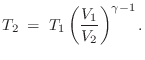
![]() is typical for any diatomic
gas.B.31 Monatomic inert gases, on the other hand,
such as Helium, Neon, and Argon, have
is typical for any diatomic
gas.B.31 Monatomic inert gases, on the other hand,
such as Helium, Neon, and Argon, have
![]() . Carbon
dioxide, which is triatomic, has a heat capacity ratio
. Carbon
dioxide, which is triatomic, has a heat capacity ratio
![]() . We see that more complex molecules have lower
. We see that more complex molecules have lower ![]() values because they can store heat in more degrees of freedom.
values because they can store heat in more degrees of freedom.




















