DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Application of the Bilinear Transform

The impedance of a mass in the frequency domain is

$\displaystyle R_M(s) = Ms. $

In the $ s$ plane, we have

$\displaystyle F_a(s) = (Ms) V_a(s) $

where the ``a'' subscript denotes ``analog''. For simplicity, let's choose the free constant $ c$ in the bilinear transform such that $ 1$ rad/sec maps to one fourth the sampling rate, i.e., $ s=j$ maps to $ z=j$ which implies $ c=1$. Then the impedance relation maps across as

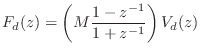
$\displaystyle F_d(z) = \left(M\frac{1-z^{-1}}{1+z^{-1}}\right) V_d(z) $

where the ``d'' subscript denotes ``digital. Multiplying through by the denominator and applying the shift theorem for $ z$ transforms gives the corresponding difference equation

\begin{eqnarray*} (1+z^{-1})F_d(z) &=& M (1-z^{-1}) V_d(z) \\ \;\longleftrighta... ... \,\,\Rightarrow\,\,f_d(n) &=& M[v_d(n) - v_d(n-1)] - f_d(n-1). \end{eqnarray*}

This difference equation is diagrammed in Fig. 7.16. We recognize this recursive digital filter as the direct form I structure. The direct-form II structure is obtained by commuting the feedforward and feedback portions and noting that the two delay elements contain the same value and can therefore be shared [449]. The two other major filter-section forms are obtained by transposing the two direct forms by exchanging the input and output, and reversing all arrows. (This is a special case of Mason's Gain Formula which works for the single-input, single-output case.) When a filter structure is transposed, its summers become branching nodes and vice versa. Further discussion of the four basic filter section forms can be found in [333].

Figure 7.16: A direct-form-I digital filter simulating a mass $ M$ created using the bilinear transform $ s=(1-z^{-1})/(1+z^{-1})$.
\includegraphics[width=4in]{eps/lmassFilterDF1}

Practical Considerations

While the digital mass simulator has the desirable properties of the bilinear transform, it is also not perfect from a practical point of view: (1) There is a pole at half the sampling rate ($ z=-1$). (2) There is a delay-free path from input to output.

The first problem can easily be circumvented by introducing a loss factor $ g$, moving the pole from $ z=-1$ to $ z=-g$, where $ g\in[0,1)$ and $ g\approx1$. This is sometimes called the ``leaky integrator''.

The second problem arises when making loops of elements (e.g., a mass-spring chain which forms a loop). Since the individual elements have no delay from input to output, a loop of elements is not computable using standard signal processing methods. The solution proposed by Alfred Fettweis is known as ``wave digital filters,'' a topic taken up in §F.1.

Next Section:
Limitations of Lumped Element Digitization
Previous Section:
Bilinear Transformation