Arctangent Series Expansion

For example, the arctangent function used above can be expanded as

Note that all even-order terms are zero. This is always the case for odd functions, i.e., functions satisfying . For any smooth function, the odd-order terms of its Taylor expansion comprise the odd part of the function, while the even-order terms comprise the even part. The original function is clearly given by the sum of its odd and even parts.^7.17

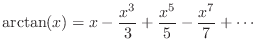
The clipping nonlinearity in Eq.(6.17) is not so amenable to a series expansion. In fact, it is its own series expansion! Since it is not differentiable at , it must be represented as three separate series over the intervals , , and , and the result obtained over these intervals is precisely the definition of in Eq.(6.17).

---

Next Section:
Spectrum of a Memoryless Nonlinearities
Previous Section:
Series Expansions

Sign in