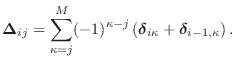Free Books    Physical Audio Signal Processing  


Boundary Conditions

The relations of the previous section do not hold exactly when the string length is finite. A finite-length string forces consideration of boundary conditions. In this section, we will introduce boundary conditions as perturbations of the state transition matrix. In addition, we will use the DW-FDTD equivalence to obtain physically well behaved boundary conditions for the FDTD method.

Consider an ideal vibrating string with $ M=8$ spatial samples. This is a sufficiently large number to make clear most of the repeating patterns in the general case. Introducing boundary conditions is most straightforward in the DW paradigm. We therefore begin with the order 8 DW model, for which the state vector (for the 0th subgrid) will be

\begin{displaymath} \underline{x}_W(n) = \left[\! \begin{array}{l} y^{+}_{n,0}\... ...}_{n,4}\\ y^{+}_{n,6}\\ y^{-}_{n,6}\\ \end{array}\!\right]. \end{displaymath}

The displacement output matrix is given by

\begin{displaymath} \mathbf{C}_W= \left[\! \begin{array}{ccccccccccc} 1 & 1 & ... ...0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \end{array}\!\right] \end{displaymath}

and the input matrix $ {\mathbf{B}_W}$ is an arbitrary $ M\times 2q$ matrix. We will choose a scalar input signal $ u(n)$ driving the displacement of the second spatial sample with unit gain:

\begin{displaymath} {\mathbf{B}_W} = \left[\! \begin{array}{cc} 0 & 0 \\ 0 & ... ... 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array}\!\right] \end{displaymath}

The state transition matrix $ \mathbf{A}_W$ is obtained by reducing Eq.$ \,$(E.32) to finite order in some way, thereby introducing boundary conditions.

Resistive Terminations

Let's begin with simple ``resistive'' terminations at the string endpoints, resulting in the reflection coefficient $ g$ at each end of the string, where $ \vert g\vert\leq 1$ corresponds to nonnegative (passive) termination resistances [447]. Inspection of Fig.E.2 makes it clear that terminating the left endpoint may be accomplished by setting

$\displaystyle y^{+}_{n,0} = g_ly^{-}_{n,0}, $

and the right termination corresponds to

$\displaystyle y^{-}_{n,6} = g_ry^{+}_{n,6}. $

By allowing an additional two samples of round-trip delay in each endpoint reflectance (one sample in the chosen subgrid), we can implement these reflections within the state-transition matrix:

$\displaystyle \tilde{\mathbf{A}}_W= \left[\! \begin{array}{ccccccccccc} 0 & g_l... ... 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & g_r & 0 \end{array} \!\right]$ (E.38)

The simplest choice of state transformation matrix $ \mathbf{T}$ is obtained by cropping it to size $ M\times M$:

\begin{displaymath} \mathbf{T}\isdef \left[\! \begin{array}{ccccccccccc} 1 & 1... ... 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\!\right] \end{displaymath}

An advantage of this choice is that its inverse $ \mathbf{T}^{-1}$ is similarly a simple cropping of the $ M=\infty$ case. However, the corresponding FDTD system is not so elegant:

\begin{eqnarray*} \tilde{\mathbf{A}}_K&\isdef & \mathbf{T}\tilde{\mathbf{A}}_W\m... ...r \\ 0 & 0 & 0 & 0 & 0 & 0 & g_r & -g_r \end{array}\!\right], \end{eqnarray*}

where $ h_l\isdef 1+g_l$ and $ h_r\isdef 1+g_r$. We see that the left FDTD termination is non-local for $ g\neq -1$, while the right termination is local (to two adjacent spatial samples) for all $ g$. This can be viewed as a consequence of having ordered the FDTD state variables as $ [y_{n,m},y_{n-1,m+1},\ldots]$ instead of $ [y_{n-1,m},y_{n,m+1},\ldots]$. Choosing the other ordering interchanges the endpoint behavior. Call these orderings Type I and Type II, respectively. Then $ \mathbf{T}_{II}=\mathbf{T}_I^T$; that is, the similarity transformation matrix $ \mathbf{T}$ is transposed when converting from Type I to Type II or vice versa. By anechoically coupling a Type I FDTD simulation on the right with a Type II simulation on the left, general resistive terminations may be obtained on both ends which are localized to two spatial samples.

In nearly all musical sound synthesis applications, at least one of the string endpoints is modeled as rigidly clamped at the ``nut''. Therefore, since the FDTD, as defined here, most naturally provides a clamped endpoint on the left, with more general localized terminations possible on the right, we will proceed with this case for simplicity in what follows. Thus, we set $ g_l=-1$ and obtain

\begin{eqnarray*} \mbox{$\stackrel{{\scriptscriptstyle \vdash}}{\mathbf{A}}$}_K&... ..._r \\ 0 & 0 & 0 & 0 & 0 & 0 & g_r & -g_r \end{array}\!\right] \end{eqnarray*}

Boundary Conditions as Perturbations

To study the effect of boundary conditions on the state transition matrices $ \mathbf{A}_W$ and $ \mathbf{A}_K$, it is convenient to write the terminated transition matrix as the sum of of the ``left-clamped'' case $ \mbox{$\stackrel{{\scriptscriptstyle \vdash}}{\mathbf{A}}$}$$ _W$ (for which $ g_l=-1$) plus a series of one or more rank-one perturbations. For example, introducing a right termination with reflectance $ g_r$ can be written

$\displaystyle \mbox{$\stackrel{{\scriptscriptstyle \vdash\!\!\dashv}}{\mathbf{A}}$}$$\displaystyle _W=$   $\displaystyle \mbox{$\stackrel{{\scriptscriptstyle \vdash}}{\mathbf{A}}$}$$\displaystyle _W+ g_r{\bm \delta}_{8,7} = \mathbf{A}_W- {\bm \delta}_{1,2} + g_r{\bm \delta}_{8,7}, \protect$ (E.39)

where $ {\bm \delta}_{ij}$ is the $ M\times M$ matrix containing a 1 in its $ (i,j)$th entry, and zero elsewhere. (Following established convention, rows and columns in matrices are numbered from 1.)

In general, when $ i+j$ is odd, adding $ {\bm \delta}_{ij}$ to $ \mbox{$\stackrel{{\scriptscriptstyle \vdash}}{\mathbf{A}}$}$$ _W$ corresponds to a connection from left-going waves to right-going waves, or vice versa (see Fig.E.2). When $ i$ is odd and $ j$ is even, the connection flows from the right-going to the left-going signal path, thus providing a termination (or partial termination) on the right. Left terminations flow from the bottom to the top rail in Fig.E.2, and in such connections $ i$ is even and $ j$ is odd. The spatial sample numbers involved in the connection are $ 2\lfloor (i-1)/2\rfloor$ and $ 2\lfloor (j-1)/2\rfloor$, where $ \lfloor x\rfloor$ denotes the greatest integer less than or equal to $ x$.

The rank-one perturbation of the DW transition matrix Eq.$ \,$(E.39) corresponds to the following rank-one perturbation of the FDTD transition matrix $ \mbox{$\stackrel{{\scriptscriptstyle \vdash}}{\mathbf{A}}$}$$ _K$:

   $\displaystyle \mbox{$\stackrel{{\scriptscriptstyle \vdash\!\!\dashv}}{\mathbf{A}}$}$$\displaystyle _K\;\isdef \;$   $\displaystyle \mbox{$\stackrel{{\scriptscriptstyle \vdash}}{\mathbf{A}}$}$$\displaystyle _K+ g{\bm \Delta}_{8,7} $

where
$\displaystyle {\bm \Delta}_{8,7}$ $\displaystyle \isdef$ \begin{displaymath}\mathbf{T}{\bm \delta}_{8,7}\mathbf{T}^{-1} = \left[\! \begin... ... 0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 \end{array}\!\right]. \protect\end{displaymath} (E.40)

In general, we have

$\displaystyle {\bm \Delta}_{ij} = \sum_{\kappa=j}^M (-1)^{\kappa-j} \left({\bm \delta}_{i\kappa}+{\bm \delta}_{i-1,\kappa}\right). \protect$ (E.41)

Thus, the general rule is that $ {\bm \delta}_{ij}$ transforms to a matrix $ {\bm \Delta}_{ij}$ which is zero in all but two rows (or all but one row when $ i=1$). The nonzero rows are numbered $ i$ and $ i-1$ (or just $ i$ when $ i=1$), and they are identical, being zero in columns $ 1:j-1$, and containing $ [1,-1,1,-1,\ldots]$ starting in column $ j$.

Reactive Terminations

In typical string models for virtual musical instruments, the ``nut end'' of the string is rigidly clamped while the ``bridge end'' is terminated in a passive reflectance $ S(z)$. The condition for passivity of the reflectance is simply that its gain be bounded by 1 at all frequencies [447]:

$\displaystyle \left\vert S(e^{j\omega T})\right\vert\leq 1, \quad \forall\, \omega T\in[-\pi,\pi). \protect$ (E.42)

A very simple case, used, for example, in the Karplus-Strong plucked-string algorithm, is the two-point-average filter:

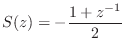
$\displaystyle S(z) = -\frac{1+z^{-1}}{2} $

To impose this lowpass-filtered reflectance on the right in the chosen subgrid, we may form

   $\displaystyle \mbox{$\stackrel{{\scriptscriptstyle \vdash\!\!\dashv}}{\mathbf{A}}$}$$\displaystyle _W=$   $\displaystyle \mbox{$\stackrel{{\scriptscriptstyle \vdash}}{\mathbf{A}}$}$$\displaystyle _W- \frac{1}{2}{\bm \Delta}_{8,5} - \frac{1}{2}{\bm \Delta}_{8,7} $

which results in the FDTD transition matrix

\begin{eqnarray*} \mbox{$\stackrel{{\scriptscriptstyle \vdash\!\!\dashv}}{\mathb... ... \\ 0 & 0 & 0 & 0 & -1/2 & 1/2 & -1 & -1 \end{array}\!\right]. \end{eqnarray*}

This gives the desired filter in a half-rate, staggered grid case. In the full-rate case, the termination filter is really

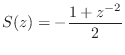
$\displaystyle S(z) = -\frac{1+z^{-2}}{2} $

which is still passive, since it obeys Eq.$ \,$(E.42), but it does not have the desired amplitude response: Instead, it has a notch (gain of 0) at one-fourth the sampling rate, and the gain comes back up to 1 at half the sampling rate. In a full-rate scheme, the two-point-average filter must straddle both subgrids.

Another often-used string termination filter in digital waveguide models is specified by [447]

\begin{eqnarray*} s(n) &=& -g\left[\frac{h}{4}, \frac{1}{2}, \frac{h}{4}\right]\... ...{j\omega T})&=& -e^{-j\omega T}g\frac{1 + h \cos(\omega T)}{2}, \end{eqnarray*}

where $ g\in(0,1)$ is an overall gain factor that affects the decay rate of all frequencies equally, while $ h\in(0,1)$ controls the relative decay rate of low-frequencies and high frequencies. An advantage of this termination filter is that the delay is always one sample, for all frequencies and for all parameter settings; as a result, the tuning of the string is invariant with respect to termination filtering. In this case, the perturbation is

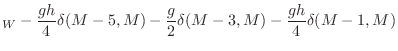
   $\displaystyle \mbox{$\stackrel{{\scriptscriptstyle \vdash\!\!\dashv}}{\mathbf{A}}$}$$\displaystyle _W=$   $\displaystyle \mbox{$\stackrel{{\scriptscriptstyle \vdash}}{\mathbf{A}}$}$$\displaystyle _W- \frac{gh}{4}\delta(M-5,M) - \frac{g}{2}\delta(M-3,M) - \frac{gh}{4}\delta(M-1,M) $

and, using Eq.$ \,$(E.41), the order $ M=8$ FDTD state transition matrix is given by

\begin{eqnarray*} \mbox{$\stackrel{{\scriptscriptstyle \vdash\!\!\dashv}}{\mathb... ...d g_2 & \quad -g_2 & \quad g_3 & \quad -g_3 \end{array}\!\right] \end{eqnarray*}

where

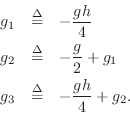
\begin{eqnarray*} g_1 &\isdef & -\frac{gh}{4}\\ g_2 &\isdef & -\frac{g}{2}+g_1\\ g_3 &\isdef & -\frac{gh}{4}+g_2.\\ \end{eqnarray*}

The filtered termination examples of this section generalize immediately to arbitrary finite-impulse response (FIR) termination filters $ S(z)$. Denote the impulse response of the termination filter by

$\displaystyle s(n)=[s_0,s_1,s_2,\ldots,s_N], $

where the length $ N$ of the filter does not exceed $ M/2$. Due to the DW-FDTD equivalence, the general stability condition is stated very simply as

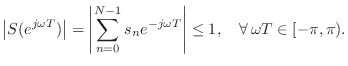
$\displaystyle \left\vert S(e^{j\omega T})\right\vert = \left\vert\sum_{n=0}^{N-1} s_n e^{-j\omega T}\right\vert \leq 1, \quad \forall\, \omega T\in[-\pi,\pi). $

Interior Scattering Junctions

A so-called Kelly-Lochbaum scattering junction [297,447] can be introduced into the string at the fourth sample by the following perturbation

   $\displaystyle \mbox{$\stackrel{{\scriptscriptstyle \rightleftharpoons}}{\mathbf{A}}$}$$\displaystyle _K=$   $\displaystyle \mbox{$\stackrel{{\scriptscriptstyle \vdash}}{\mathbf{A}}$}$$\displaystyle _K+ (1-k_l){\bm \Delta}_{5,3} + k_r {\bm \Delta}_{5,8} + k_l {\bm \Delta}_{6,3} + (1-k_r){\bm \Delta}_{6,8}. $

Here, $ k_l$ denotes the reflection coefficient ``seen'' from left to right, and $ k_r$ is the reflectance of the junction from the right. When the scattering junction is caused by a change in string density or tension, we have $ k_r=-k_l$. When it is caused by an externally imposed termination (such as a plectrum or piano-hammer touching the string), we have $ k_r=k_l$, and the reflectances may become filters instead of real values in $ [-1,1]$. Energy conservation demands that the transmission coefficients be amplitude complementary with respect to the reflection coefficients [447].

A single time-varying scattering junction provides a reasonable model for plucking, striking, or bowing a string at a point. Several adjacent scattering junctions can model a distributed interaction, such as a piano hammer, finger, or finite-width bow spanning several string samples.

Note that scattering junctions separated by one spatial sample (as typical in ``digital waveguide filters'' [447]) will couple the formerly independent subgrids. If scattering junctions are confined to one subgrid, they are separated by two samples of delay instead of one, resulting in round-trip transfer functions of the form $ H(z^2)$ (as occurs in the digital waveguide mesh). In the context of a half-rate staggered-grid scheme, they can provide general IIR filtering in the form of a ladder digital filter [297,447].

Next Section:
Lossy Vibration
Previous Section:
DW State Space Model