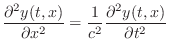DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Characteristic Polynomial Equation

The characteristic polynomial equation for a linear PDE with constant coefficients is obtained by taking the 2D Laplace transform of the PDE with respect to $ x$ and $ t$. A simple way of doing this is to substitute the general eigensolution

$\displaystyle y(t,x) = e^{st+vx}$ (D.6)

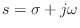
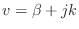
into the PDE, where $ s=\sigma+j\omega$ denotes the complex variable associated with the Laplace-transform with respect to time, and $ v=\beta+jk$ is the complex variable associated with the spatial Laplace transform.

As a simple example, the ideal-string wave equation (analyzed in §C.1) is a simple second-order PDE given by

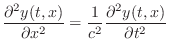$\displaystyle \frac{\partial^2 y(t,x)}{\partial x^2} = \frac{1}{c^2} \frac{\partial^2 y(t,x)}{\partial t^2} \protect$ (D.7)

where $ c$ is a positive constant (sound speed, as discussed in §C.1).

Substituting Eq.$ \,$(D.6) into Eq.$ \,$(D.7) results in the following characteristic polynomial equation:

$\displaystyle v^2 - \frac{1}{c^2}s^2 = 0 $

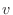
Solving for $ s$ in terms of $ v$ gives the so-called dispersion relation:

$\displaystyle s = \pm c v $

or, looking only at the frequency axes (i.e., using Fourier transforms in place of Laplace transforms),

$\displaystyle \omega = \pm c k. $

Since the phase velocity of a traveling wave is, by definition, the temporal frequency divided by spatial frequency, we have simply

$\displaystyle v_p \isdef \frac{\omega}{k} = \pm c. $

This result can be interpreted as saying that all Fourier components of any solution of Eq.$ \,$(D.7) must propagate along the string with speed $ c$ to either the left or the right along the string. In more general PDEs, propagation may be dispersive, in which case the phase velocity depends on frequency (see §C.6 for an analysis of stiff vibrating strings, which are dispersive). Moreover, wave propagation may be damped in a frequency-dependent way, in which case one or more roots of the characteristic polynomial equation will have negative real parts; if any roots have positive real parts, we say the initial-value problem is ill posed since is has exponentially growing solutions in response to initial conditions.

Next Section:
Von Neumann Analysis
Previous Section:
Convergence