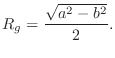Free Books    Physical Audio Signal Processing  

Circular Cross-Section

For a circular cross-section of radius $ a$, Eq.$ \,$(B.11) tells us that the squared radius of gyration about any line passing through the center of the cross-section is given by

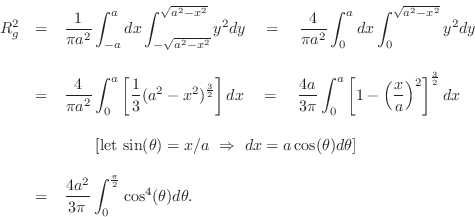
\begin{eqnarray*} R_g^2 &=& \frac{1}{\pi a^2} \int_{-a}^a dx \int_{-\sqrt{a^2-x^... ...frac{4a^2}{3\pi} \int_{0}^{\frac{\pi}{2}} \cos^4(\theta)d\theta. \end{eqnarray*}

Using the elementrary trig identity $ \cos(2\theta)=2\cos^2(\theta)-1$, we readily derive

$\displaystyle \cos^4(\theta) = \frac{1}{8}\cos(4\theta) + \frac{1}{2}\cos(2\theta) + \frac{3}{8}. $

The first two terms of this expression contribute zero to the integral from 0 to $ \pi /2$, while the last term contributes $ 3\pi/16$, yielding

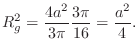
$\displaystyle R_g^2 = \frac{4a^2}{3\pi} \frac{3\pi}{16} = \frac{a^2}{4}. $

Thus, the radius of gyration about any midline of a circular cross-section of radius $ a$ is

$\displaystyle R_g = \frac{a}{2}. $

For a circular tube in which the mass of the cross-section lies within a circular annulus having inner radius $ b$ and outer radius $ a$, the radius of gyration is given by

$\displaystyle R_g = \frac{\sqrt{a^2-b^2}}{2}. \protect$ (B.12)

Next Section:
Striking the Rod in the Middle
Previous Section:
Rectangular Cross-Section