Clarinet Synthesis Implementation Details
To finish off the clarinet example, the remaining details of the SynthBuilder clarinet patch Clarinet2.sb are described.
The input mouth pressure is summed with a small amount of white noise,
corresponding to turbulence. For example, 0.1% is generally used as a
minimum, and larger amounts are appropriate during the attack of a note.
Ideally, the turbulence level should be computed automatically as a
function of pressure drop
![]() and reed opening geometry
[141,530]. It should also be lowpass filtered
as predicted by theory.
and reed opening geometry
[141,530]. It should also be lowpass filtered
as predicted by theory.
Referring to Fig. 9.39, the reflection filter is a simple one-pole with transfer function
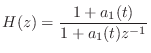 |
(10.50) |
where
Legato note transitions are managed using two delay line taps and cross-fading from one to the other during a transition [208,441,405]. In general, legato problems arise when the bore length is changed suddenly while sounding, corresponding to a new fingering. The reason is that really the model itself should be changed during a fingering change from that of a statically terminated bore to that of a bore with a new scattering junction appearing where each ``finger'' is lifting, and with disappearing scattering junctions where tone holes are being covered. In addition, if a hole is covered abruptly (especially when there are large mechanical caps, as in the saxophone), there will also be new signal energy injected in both directions on the bore in superposition with the signal scattering. As a result of this ideal picture, is difficult to get high quality legato performance using only a single delay line.
A reduced-cost, approximate solution for obtaining good sounding note transitions in a single delay-line model was proposed in [208]. In this technique, the bore delay line is ``branched'' during the transition, i.e., a second feedback loop is formed at the new loop delay, thus forming two delay lines sharing the same memory, one corresponding to the old pitch and the other corresponding to the new pitch. A cross-fade from the old-pitch delay to the new-pitch delay sounds good if the cross-fade time and duration are carefully chosen. Another way to look at this algorithm is in terms of ``read pointers'' and ``write pointers.'' A normal delay line consists of a single write pointer followed by a single read pointer, delayed by one period. During a legato transition, we simply cross-fade from a read-pointer at the old-pitch delay to a read-pointer at the new-pitch delay. In this type of implementation, the write-pointer always traverses the full delay memory corresponding to the minimum supported pitch in order that read-pointers may be instantiated at any pitch-period delay at any time. Conceptually, this simplified model of note transitions can be derived from the more rigorous model by replacing the tone-hole scattering junction by a single reflection coefficient.
STK software implementing a model as in Fig.9.39 can be found in the file Clarinet.cpp.
Next Section:
The Clarinet Tonehole as a Two-Port Junction
Previous Section:
Computational Methods




















