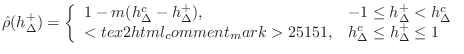Computational Methods
Since finding the intersection of ![]() and
and
![]() requires an expensive
iterative algorithm with variable convergence times, it is not well suited
for real-time operation. In this section, fast algorithms based on
precomputed nonlinearities are described.
requires an expensive
iterative algorithm with variable convergence times, it is not well suited
for real-time operation. In this section, fast algorithms based on
precomputed nonlinearities are described.
Let ![]() denote half-pressure
denote half-pressure ![]() , i.e.,
, i.e.,
![]() and
and
![]() . Then (9.43) becomes
. Then (9.43) becomes
Subtracting this equation from
The last expression above can be used to precompute
| (10.47) |
(9.45) becomes
This is the form chosen for implementation in Fig. 9.39 [431]. The control variable is mouth half-pressure
Because the table contains a coefficient rather than a signal value, it
can be more heavily quantized both in address space and word length than
a direct lookup of a signal value such as
![]() or the like. A
direct signal lookup, though requiring much higher resolution, would
eliminate the multiplication associated with the scattering coefficient.
For example, if
or the like. A
direct signal lookup, though requiring much higher resolution, would
eliminate the multiplication associated with the scattering coefficient.
For example, if ![]() and
and ![]() are 16-bit signal samples,
the table would contain on the order of 64K 16-bit
are 16-bit signal samples,
the table would contain on the order of 64K 16-bit
![]() samples.
Clearly, some compression of this table would be desirable. Since
samples.
Clearly, some compression of this table would be desirable. Since
![]() is smoothly varying, significant compression is in fact
possible. However, because the table is directly in the signal path,
comparatively little compression can be done while maintaining full
audio quality (such as 16-bit accuracy).
is smoothly varying, significant compression is in fact
possible. However, because the table is directly in the signal path,
comparatively little compression can be done while maintaining full
audio quality (such as 16-bit accuracy).
In the field of computer music, it is customary to use simple piecewise linear functions for functions other than signals at the audio sampling rate, e.g., for amplitude envelopes, FM-index functions, and so on [382,380]. Along these lines, good initial results were obtained [431] using the simplified qualitatively chosen reed table
depicted in Fig. 9.42 for
Another variation is to replace the table-lookup contents by a piecewise polynomial approximation. While less general, good results have been obtained in practice [89,91,92]. For example, one of the SynthBuilder [353] clarinet patches employs this technique using a cubic polynomial.
An intermediate approach between table lookups and polynomial approximations is to use interpolated table lookups. Typically, linear interpolation is used, but higher order polynomial interpolation can also be considered (see Chapter 4).
Next Section:
Clarinet Synthesis Implementation Details
Previous Section:
Scattering-Theoretic Formulation








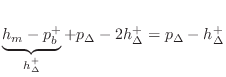
![\includegraphics[width=4in]{eps/fReedTable}](http://www.dsprelated.com/josimages_new/pasp/img2382.png)