Free Books    Physical Audio Signal Processing  

Consistency

A finite-difference scheme is said to be consistent with the original partial differential equation if, given any sufficiently differentiable function $ y(t,x)$, the differential equation operating on $ y(t,x)$ approaches the value of the finite difference equation operating on $ y(nT,mX)$, as $ T$ and $ X$ approach zero.

Thus, in the ideal string example, to show the consistency of Eq.$ \,$(D.3) we must show that

$\displaystyle \left(\frac{\partial^2}{\partial x^2} - \frac{1}{c^2} \frac{\par... ...eft[ (\delta_x + \delta_x^{-1}) - (\delta_t + \delta_t^{-1}) \right] y_{n,m} $

for all $ y(t,x)$ which are second-order differentiable with respect to $ t$ and $ x$. On the right-hand side, we have introduced the following shift operator notation:
$\displaystyle \delta_t^k y_{n,m}$ $\displaystyle \isdef$ $\displaystyle y_{n-k,m}$  
$\displaystyle \delta_x^k y_{n,m}$ $\displaystyle \isdef$ $\displaystyle y_{n,m-k} \protect$ (D.4)

In particular, we have

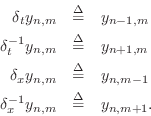
\begin{eqnarray*} \delta_t y_{n,m}&\isdef & y_{n-1,m}\\ \delta_t^{-1} y_{n,m}&\... ...&\isdef & y_{n,m-1}\\ \delta_x^{-1} y_{n,m}&\isdef & y_{n,m+1}. \end{eqnarray*}

In taking the limit as $ T$ and $ X$ approach zero, we must maintain the relationship $ X=cT$, and we must scale the FDS by $ 1/X^2$ in order to achieve an exact result:

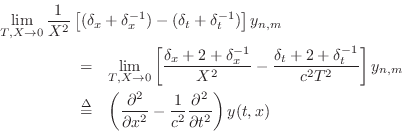
\begin{eqnarray*} \lefteqn{\lim_{T,X\to0} \frac{1}{X^2} \left[ (\delta_x + \del... ... - \frac{1}{c^2} \frac{\partial^2}{\partial t^2} \right)y(t,x) \end{eqnarray*}

as required. Thus, the FDS is consistent. See, e.g., [481] for more examples.

In summary, consistency of a finite-difference scheme means that, in the limit as the sampling intervals approach zero, the original PDE is obtained from the FDS.

Next Section:
Well Posed Initial-Value Problem
Previous Section:
Cylinder with Conical Cap