Cylindrical Tubes

In the case of cylindrical tubes, the logarithmic derivative of the area variation, ln, is zero, and Eq.(C.148) reduces to the usual momentum conservation equation encountered when deriving the wave equation for plane waves [318,349,47]. The present case reduces to the cylindrical case when

i.e., when the relative change in cross-sectional area is much less than the relative change in pressure along the tube. In other words, the tube area variation must be slower than the spatial variation of the wave itself. This assumption is also necessary for the ``one-parameter-wave'' approximation to hold in the first place.

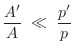
If we look at sinusoidal spatial waves, and , then and , and the condition for cylindrical-wave behavior becomes , i.e., the spatial frequency of the wall variation must be much less than that of the wave. Another way to say this is that the wall must be approximately flat across a wavelength. This is true for smooth horns/bores at sufficiently high wave frequencies.

---

Next Section:
Scattering Filters at the Cylinder-Cone Junction
Previous Section:
Digital Simulation

Sign in