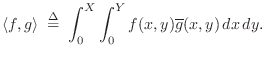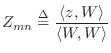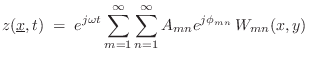DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

2D Boundary Conditions

We often wish to find solutions of the 2D wave equation that obey certain known boundary conditions. An example is transverse waves on an ideal elastic membrane, rigidly clamped on its boundary to form a rectangle with dimensions 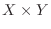$ X\times Y$ meters.

Similar to the derivation of Eq.$ \,$(B.49), we can subtract the second sinusoidal traveling wave from the first to yield

$\displaystyle z(\underline{x},t) \eqsp A\,e^{j\phi}\,e^{j\omega t - kx} - A\,e^{j\phi}\,e^{j\omega t + kx} \eqsp 2A\,e^{j(\omega t + \phi+\pi/2)}\,\sin(kx) $

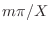
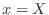
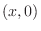
which satisfies the zero-displacement boundary condition along the $ y$ axis. If we restrict the wavenumber $ k$ to the set $ m\pi/X$, where $ m$ is any positive integer, then we also satisfy the boundary condition along the line parallel to the $ y$ axis at $ x=X$. Similar standing waves along $ y$ will satisfy both boundary conditions along $ (x,0)$ and $ (x,Y)$.

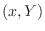
Note that we can also use products of horizontal and vertical standing waves

$\displaystyle z(\underline{x},t) \eqsp A\,e^{j\omega t + \phi}\,\sin(kx)\sin(ky) $

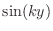
because, when taking the partial derivative with respect to $ x$, the term $ \sin(ky)$ is simply part of the constant coefficient, and vice versa.

To build solutions to the wave equation that obey all of the boundary conditions, we can form linear combinations of the above standing-wave products having zero displacement (``nodes'') along all four boundary lines:

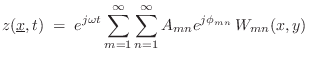$\displaystyle z(\underline{x},t) \eqsp e^{j\omega t} \sum_{m=1}^{\infty}\sum_{n=1}^{\infty} A_{mn}e^{j\phi_{mn}}\,W_{mn}(x,y) \protect$ (B.50)

where

$\displaystyle W_{mn}(x,y) \isdefs \sin\left(m\frac{\pi}{X}x\right)\sin\left(n\frac{\pi}{Y}y\right). $

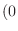
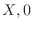
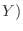
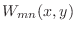
By construction, all linear combinations of the form Eq.$ \,$(B.50) are solutions of the wave equation that satisfy the zero boundary conditions along the rectangle $ (0$-$ X,0$-$ Y)$. Since sinusoids at different frequencies are orthogonal, the solution building-blocks $ W_{mn}(x,y)$ are orthogonal under the inner product

$\displaystyle \left<f,g\right> \isdefs \int_0^X\int_0^Y f(x,y)\overline{g}(x,y)\,dx\,dy. $

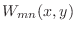
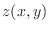
It remains to be shown that the set of functions $ W_{mn}(x,y)$ is complete, that is, that they form a basis for the set of all solutions to the wave equation satisfying the boundary conditions. Given that, we can solve the problem of arbitrary initial conditions. That is, given any initial $ z(x,y)$ over the membrane (subject to the boundary conditions, of course), we can find the amplitude of each excited mode by simple projection:

$\displaystyle Z_{mn} \isdef \frac{\left<z,W\right>}{\left<W,W\right>} $

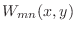
Showing completeness of the basis $ W_{mn}(x,y)$ in the desired solution space is a special case (zero boundary conditions) of the problem of showing that the 2D Fourier series expansion is complete in the space of all continuous rectangular surfaces.

The Wikipedia page (as of 1/31/10) on the Helmholtz equation provides a nice ``entry point'' on the above topics and further information.

Next Section:
3D Sound
Previous Section:
Solving the 2D Wave Equation