3D Sound
The mathematics of 3D sound is quite elementary, as we will see below. The hard part of the theory of practical systems typically lies in the mathematical approximation to the ideal case. Examples include Ambisonics [158] and wave field synthesis [49].
Consider a point source at position
. Then the
acoustic complex amplitude at position
is given by
denotes the complex amplitude one meter from the
point source in any direction, and
denotes the wavenumber
(spatial radian frequency). Distributed acoustic sources are
handled as a superposition of point sources, so the point source is a
completely general building block for all types of sources in linear
acoustics.
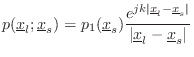
The fundamental approximation problem in 3D sound is to approximate
the complex acoustic field at one or more listening points using a
finite set of 
loudspeakers, which are often modeled as a point
source for each speaker.
Next Section:
FDA of the Ideal String
Previous Section:
2D Boundary Conditions
