Free Books
   Free Books    Physical Audio Signal Processing  

Damping and Tuning Parameters

The tuning and damping of the resonator impulse response are governed by the relation

$\displaystyle {\lambda_i}= e^{\frac{T}{\tau}} e^{\pm j\omega T} $

where $ T$ denotes the sampling interval, $ \tau $ is the time constant of decay, and $ \omega $ is the frequency of oscillation in radians per second. The eigenvalues are presumed to be complex, which requires, from Eq.$ \,$(C.144),

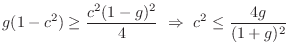
$\displaystyle g(1-c^2) \geq\frac{c^2(1-g)^2}{4} \,\,\Rightarrow\,\,c^2 \leq \frac{4g}{(1+g)^2} $

To obtain a specific decay time-constant $ \tau $, we must have

\begin{eqnarray*} e^{-2T/\tau} &=& \left\vert{\lambda_i}\right\vert^2 = c^2\left... ...left[g(1-c^2) - c^2\left(\frac{1-g}{2}\right)^2\right]\\ &=& g \end{eqnarray*}

Therefore, given a desired decay time-constant $ \tau $ (and the sampling interval $ T$), we may compute the damping parameter $ g$ for the digital waveguide resonator as

$\displaystyle \zbox {g = e^{-2T/\tau}.} $

Note that this conclusion follows directly from the determinant analysis of Eq.$ \,$(C.140), provided it is known that the poles form a complex-conjugate pair.

To obtain a desired frequency of oscillation, we must solve

\begin{eqnarray*} \theta = \omega T &=& \tan^{-1}\left[\frac{\sqrt{g(1-c^2) - [... ...,\tan^2{\theta} &=& \frac{g(1-c^2) - [c(1-g)/2]^2}{[c(1+g)/2]^2} \end{eqnarray*}

for $ c$, which yields

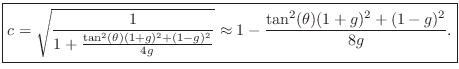
$\displaystyle \zbox { c= \sqrt{\frac{1}{1 + \frac{\tan^2(\theta)(1+g)^2+(1-g)^2}{4g}}} \approx 1 - \frac{\tan^2(\theta)(1+g)^2 + (1-g)^2}{8g}. } $

Note that this reduces to $ c=\cos(\theta)$ when $ g=1$ (undamped case).

Next Section:
Eigenvalues in the Undamped Case
Previous Section:
Miscellaneous Properties