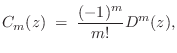Differentiator Filter Bank
Since, in the time domain, a Taylor series expansion of
 about time
about time  gives
gives
where 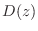 denotes the transfer function of the ideal differentiator,
we see that the
denotes the transfer function of the ideal differentiator,
we see that the  th filter in Eq.
th filter in Eq. (4.10) should approach
(4.10) should approach
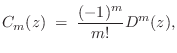 |
(5.12) |
in the limit, as the number of terms

goes to infinity.
In other terms, the coefficient

of
in the polynomial
expansion Eq.

(
4.10) must become proportional to the
 th-order differentiator
th-order differentiator as the polynomial order increases.
For any finite

, we expect

to be close to some scaling of
the

th-order differentiator. Choosing

as in Eq.

(
4.12)
for finite

gives a
truncated Taylor series approximation of
the ideal delay operator in the time domain [
184, p. 1748].
Such an approximation is ``maximally smooth'' in the time domain, in
the sense that the first

derivatives of the interpolation error
are zero at
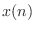
.
5.6 The
approximation
error in the time domain can be said to be
maximally flat.
Farrow structures such as Fig.4.19 may be used to implement any
one-parameter filter variation in terms of several constant
filters. The same basic idea of polynomial expansion has been applied
also to time-varying filters (
 ).
).
Next Section: Choice of Table Size and Word LengthsPrevious Section: Farrow Structure Coefficients
![]() about time
about time ![]() gives
gives
![\begin{eqnarray*}
x(n-\Delta)
&=& x(n) -\Delta\, x^\prime(n)
+ \frac{\Delta^2...
...D^2(z) + \cdots
+ \frac{(-\Delta)^k}{k!}D^k(z) + \cdots \right]
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img1101.png)
![]() denotes the transfer function of the ideal differentiator,
we see that the
denotes the transfer function of the ideal differentiator,
we see that the ![]() th filter in Eq.
th filter in Eq.![]() (4.10) should approach
(4.10) should approach
![]() ).
).