DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Digital Simulation

A discrete-time simulation of the above solution may be obtained by simply sampling the traveling-wave amplitude at intervals of $ T$ seconds, which implies a spatial sampling interval of $ X\isdeftext cT$ meters. Sampling is carried out mathematically by the change of variables

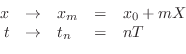
\begin{displaymath} \begin{array}{rclrl} x& \to & x_m&=& x_0+ mX\\ t & \to & t_n&=& nT \end{array}\end{displaymath}

and this substitution in Eq.$ \,$(C.146) gives

\begin{eqnarray*} x_mp(t_n,x_m) &\,\mathrel{\mathop=}\,& f(t_n- x_m/c)+g(t_n+ x... ...hop=}\,& f\left[(n-m)T-x_0/c\right]+ g\left[(n+m)T+x_0/c\right]. \end{eqnarray*}

Define

$\displaystyle p^+(n) \isdef f(nT-x_0/c) \qquad\qquad p^-(n) \isdef g(nT+x_0/c) $

where $ x_0$ is arbitrarily chosen as the position along the cone closest to the tip. (We avoid a sample at the tip itself, where a pressure singularity may exist.) Then a section of the ideal cone can be simulated as shown in Figure C.43 (where pressure outputs are shown for $ x=x_0$ and $ x=x_0+3X$). A particle-velocity output is formed by dividing the traveling pressure waves by the wave impedance of air. Since the wave impedance is now a function of frequency and propagation direction (as derived below), a digital filter will replace what was a real number for cylindrical tubes.

Figure C.43: Digital simulation of the ideal, lossless, conical waveguide with observation points at $ x=x_0$ and $ x=x_0+3X=x_0+3cT$. The symbol ``$ z^{-1}$'' denotes a one-sample delay.
\includegraphics[width=\twidth]{eps/fcideal}

A more compact simulation diagram which stands for either sampled or continuous simulation is shown in Figure C.44. The figure emphasizes that the ideal, lossless waveguide is simulated by a bidirectional delay line.

Figure C.44: Simplified picture of ideal waveguide simulation.
\includegraphics[width=\twidth]{eps/fcone}

As in the case of uniform waveguides, the digital simulation of the traveling-wave solution to the lossless wave equation in spherical coordinates is exact at the sampling instants, to within numerical precision, provided that the traveling waveshapes are initially bandlimited to less than half the sampling frequency. Also as before, bandlimited interpolation can be used to provide time samples or position samples at points off the simulation grid. Extensions to include losses, such as air absorption and thermal conduction, or dispersion, can be carried out as described in §2.3 and §C.5 for plane-wave propagation (through a uniform wave impedance).

The simulation of Fig.C.44 suffices to simulate an isolated conical frustum, but what if we wish to interconnect two or more conical bores? Even more importantly, what driving-point impedance does a mouthpiece ``see'' when attached to the narrow end of a conical bore? The preceding only considered pressure-wave behavior. We must now also find the velocity wave, and form their ratio to obtain the driving-point impedance of a conical tube.

Next Section:
Cylindrical Tubes
Previous Section:
Back to the Cone