Free Books    Physical Audio Signal Processing  

Digitizing Bridge Reflectance

Converting continuous-time transfer functions such as $ \hat{\rho}_b(s)$ and $ \hat{\tau}_b(s)$ to the digital domain is analogous to converting an analog electrical filter to a corresponding digital filter--a problem which has been well studied [343]. For this task, the bilinear transform (§7.3.2) is a good choice. In addition to preserving order and being free of aliasing, the bilinear transform preserves the positive-real property of passive impedances (§C.11.2).

Digitizing $ \hat{\rho}_b(s)$ via the bilinear transform (§7.3.2) transform gives

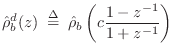
$\displaystyle \hat{\rho}_b^d(z) \isdefs \hat{\rho}_b\left(c\frac{1-z^{-1}}{1+z^{-1}}\right) $

which is a second-order digital filter having gain less than one at all frequencies--i.e., it is a Schur filter that becomes an allpass as the damping $ \mu $ approaches zero. The choice of bilinear-transform constant $ c=1/\tan(\omega_0T/2)$ maps the peak-frequency $ \omega_0$ without error (see Problem 4).

Next Section:
A Two-Resonance Guitar Bridge
Previous Section:
Bridge Transmittance