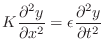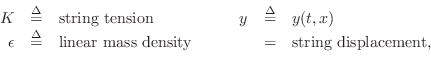Free Books
   Free Books    Physical Audio Signal Processing  

Early Musical Acoustics

All things which can be known have number; for it is not possible that without number anything can be either conceived or known.
-- Philolaus (ca. 400 BC)

Vibrating strings were studied by the Pythagoreans (6th-5th century BC). Pythagorus noticed that harmonics were produced by dividing the string length by whole numbers, and he was interested in understanding consonant pitch intervals in terms of simple ratios of string lengths. ``Harmony theory'' from the Pythagoreans was taught throughout the Middle Ages as one of the seven liberal arts: the quadrivium, consisting of arithmetic, geometry, astronomy, and music (harmony theory); and the trivium, consisting of grammar, logic, and rhetoric [411]. The correspondence between musical pitch and frequency of physical vibration was not discovered until the seventeenth century [113]. It took until Galileo (1564-1642) to be free of the formulation of Aristotle (384-322 BC) that all motion required an ongoing applied force, thereby opening the way for modern differential equations of motion. The ideas of Galileo were formalized and extended by Newton (1642-1727), whose famous second law of motion ``$ f=ma$'' lies at the foundation of essentially all classical mechanics and acoustics. Newton's Principia (1686) describes sound as traveling pressure pulses, and single-frequency sound waves were analyzed. The first to publish a one-dimensional wave equation for the vibrating string was the applied mathematician Jean Le Rond d'Alembert (1717-1783) [100,103].A.1The 1D wave equation can be written as

$\displaystyle K\frac{\partial^2 y}{\partial x^2} = \epsilon\frac{\partial^2 y}{\partial t^2}$ (A.1)

where

\begin{displaymath}\begin{array}{rclrcl} K & \isdef & \mbox{string tension} & \q... ...r mass density} & & = & \mbox{string displacement}, \end{array}\end{displaymath}    

$ t$ is time in seconds, and $ x$ denotes position along the string. (See discussion in §C.1.) It can be derived directly from Newton's second law applied to a differential string element by equating the string restoring force about a small element (first described by Brook Taylor in 1713) to Newton's mass times acceleration of that element, which is how d'Alembert in fact proceeded in his derivation [103]. In addition to introducing the 1D wave equation as an equation among differentials, d'Alembert derived its solution in terms of traveling waves:

$\displaystyle y(t,x) = y_r\left(t-\frac{x}{c}\right) + y_l\left(t+\frac{x}{c}\right)$ (A.2)

where $ c=\sqrt{K/\epsilon }$ denotes the wave propagation speed. Earlier, in 1717, Brook Taylor (1685-1731)A.2published what was apparently the first mathematical paper on vibrating strings, but without introducing differential equations. D'Alembert's ideas were developed into essentially modern form primarily by Euler (1707-1783)A.3 [65]. Incidentally, d'Alembert also invented the theory of construction of eyeglasses.A.4
Next Section:
History of Modal Expansion
Previous Section:
Other Instruments