Free Books    Physical Audio Signal Processing  

Energy Density Waves

The vibrational energy per unit length along the string, or wave energy density [317] is given by the sum of potential and kinetic energy densities:

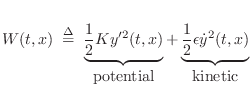$\displaystyle W(t,x) \isdefs \underbrace{\frac{1}{2} Ky'^2(t,x)}_{\mbox{potential}} + \underbrace{\frac{1}{2} \epsilon {\dot y}^2(t,x)}_{\mbox{kinetic}}$ (C.50)

Sampling across time and space, and substituting traveling wave components, one can show in a few lines of algebra that the sampled wave energy density is given by

$\displaystyle W(t_n,x_m) \isdefs W^{+}(n-m) + W^{-}(n+m),$ (C.51)

where

\begin{eqnarray*} W^{+}(n) &=& \frac{{\cal P}^{+}(n)}{c} \,\mathrel{\mathop=}\,\... ...ht]^2 \,\mathrel{\mathop=}\,\frac{\left[f^{{-}}(n)\right]^2}{K}. \end{eqnarray*}

Thus, traveling power waves (energy per unit time) can be converted to energy density waves (energy per unit length) by simply dividing by $ c$, the speed of propagation. Quite naturally, the total wave energy in the string is given by the integral along the string of the energy density:

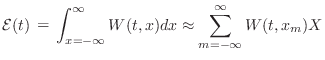$\displaystyle {\cal E}(t) \,\mathrel{\mathop=}\,\int_{x=-\infty}^\infty W(t,x)dx \approx \sum_{m = -\infty}^\infty W(t,x_m)X$ (C.52)

In practice, of course, the string length is finite, and the limits of integration are from the $ x$ coordinate of the left endpoint to that of the right endpoint, e.g., 0 to $ L$.

Next Section:
Root-Power Waves
Previous Section:
Power Waves