Force or Pressure Waves at a Rigid Termination
To find out how force or pressure waves recoil from a rigid
termination, we may convert velocity waves to force or velocity waves
by means of the Ohm's law relations of Eq.![]() (6.6) for strings
(or Eq.
(6.6) for strings
(or Eq.![]() (6.7) for acoustic tubes), and then use
Eq.
(6.7) for acoustic tubes), and then use
Eq.![]() (6.12), and then Eq.
(6.12), and then Eq.![]() (6.6) again:
(6.6) again:

Thus, force (and pressure) waves reflect from a rigid termination with no sign inversion:7.3
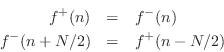
The reflections from a rigid termination in a digital-waveguide acoustic-tube simulation are exactly analogous:
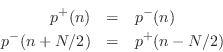
Waveguide terminations in acoustic stringed and wind instruments are never perfectly rigid. However, they are typically passive, which means that waves at each frequency see a reflection coefficient not exceeding 1 in magnitude. Aspects of passive ``yielding'' terminations are discussed in §C.11.
Next Section:
Digital Waveguide Equivalent Circuits
Previous Section:
Velocity Waves at a Rigid Termination




















