DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Force Wave Mass-String Model

The velocity transmittance is readily converted to a force transmittance using the Ohm's-law relations:

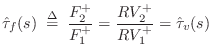
$\displaystyle \hat{\tau}_f(s) \isdefs \frac{F^{+}_2}{F^{+}_1} = \frac{RV^{+}_2}{RV^{+}_1} = \hat{\tau}_v(s) $

Calculating it for the other direction as a check gives

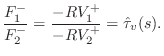
$\displaystyle \frac{F^{-}_1}{F^{-}_2} = \frac{-RV^{+}_1}{-RV^{+}_2} = \hat{\tau}_v(s). $

Thus, while the reflectance of the mass toggles sign when going from force to velocity waves, the transmittance of the mass is the same in all cases. We therefore have the force-wave scattering junction shown in Fig.9.19.

Figure 9.19: Force-wave scattering junction representing a mass $ m$ (impedance $ ms$) attached to an ideal string having wave impedance $ R$.
\includegraphics[width=0.8\twidth]{eps/massstringdwmformforce}

Checking as before, we see that $ m\to\infty$ corresponds to $ \hat{\tau}_v(s)\to 0$, which means no force is transmitted through an infinite mass, which is reasonable. As $ m\to0$, the force transmittance becomes 1 and the mass has no effect, as desired.

Next Section:
Summary of Mass-String Scattering Junction
Previous Section:
Mass Transmittance from String to String