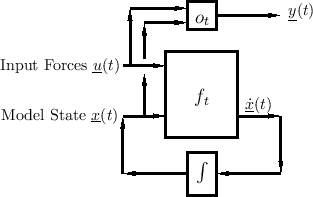
Forming Outputs

Any system output is some function of the state, and possibly the input (directly):

$\displaystyle \underline{y}(t) \isdef o_t[\underline{x}(t),\underline{u}(t)]$

The general case of output extraction is shown in Fig.1.5.

**Figure:** Continuous-time state-space model with output vector $\underline{y}(t) = o_t[\underline{x}(t),\underline{u}(t)]$ .
$\includegraphics{eps/statespaceanalogwo}$

The output signal (vector) is most typically a linear combination of state variables and possibly the current input:

$\displaystyle \underline{y}(t) \isdefs C\underline{x}(t) + D\underline{u}(t)$

where

and

are constant matrices of linear-combination coefficients.

Next Section:
State-Space Model of a Force-Driven Mass

Sign in