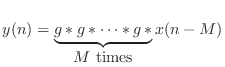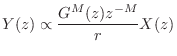Free Books    Physical Audio Signal Processing  

Frequency-Dependent Air-Absorption Filtering

More generally, frequency-dependent air absorption can be modeled using the substitution

$\displaystyle z^{-1}\leftarrow G(z)z^{-1} $

where $ G(z)$ denotes the filtering per sample in the propagation medium. Since air absorption cannot amplify a wave at any frequency, we have $ \left \vert G(e^{j\omega T})\right \vert\leq 1$. A lossy delay line for plane-wave simulation is thus described by

$\displaystyle Y(z) = G^M(z) z^{-M}X(z) $

in the frequency domain, and

$\displaystyle y(n) = \underbrace{g\ast g\ast \dots \ast g \, \ast }_{\hbox{$M$\ times}} x(n-M) $

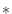
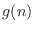
in the time domain, where `$ \ast $' denotes convolution, and $ g(n)$ is the impulse response of the per-sample loss filter $ G(z)$. The effect of $ G(z)$ on the poles of the system is discussed in §3.7.4.

For spherical waves, the loss due to spherical spreading is of the form

$\displaystyle Y(z) \propto \frac{G^M(z) z^{-M}}{r}X(z) $

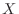
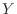
where $ r$ is the distance from $ X$ to $ Y$. We see that the spherical spreading loss factor is ``hyperbolic'' in the propagation distance $ r$, while air absorption is exponential in $ r$.

Next Section:
Dispersive Traveling Waves
Previous Section:
Exponentially Decaying Traveling Waves