Heat Capacity of Ideal Gases

In statistical thermodynamics [175,138], it is derived that each molecular degree of freedom contributes to the molar heat capacity of an ideal gas, where again is the ideal gas constant.

An ideal monatomic gas molecule (negligible spin) has only three degrees of freedom: its kinetic energy in the three spatial dimensions. Therefore, . This means we expect

a result that agrees well with experimental measurements [138].

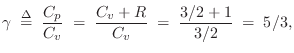
For an ideal diatomic gas molecule such as air, which can be pictured as a ``bar bell'' configuration of two rubber balls, two additional degrees of freedom are added, both associated with spinning the molecule about an axis orthogonal to the line connecting the atoms, and piercing its center of mass. There are two such axes. Spinning about the connecting axis is neglected because the moment of inertia is so much smaller in that case. Thus, for diatomic gases such as dry air, we expect

as observed to a good degree of approximation at normal temperatures. At high temperatures, new degrees of freedom appear associated with vibrations in the molecular bonds. (For example, the ``bar bell'' can vibrate longitudinally.) However, such vibrations are ``frozen out'' at normal room temperatures, meaning that their (quantized) energy levels are too high and spaced too far apart to be excited by room temperature collisions [138, p. 147].^B.32

---

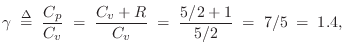
Next Section:
Speed of Sound in Air
Previous Section:
Adiabatic Gas Constant

Sign in