Free Books
   Free Books    Physical Audio Signal Processing  

Householder Reflections

For completeness, this section derives the Householder reflection matrix from geometric considerations [451]. Let $ \mathbf{P}_{\underline{u}}$ denote the projection matrix which orthogonally projects vectors onto $ {\underline{u}}$, i.e.,

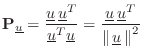
$\displaystyle \mathbf{P}_{\underline{u}}= \frac{\underline{u}\,\underline{u}^T}... ...frac{\underline{u}\,\underline{u}^T}{\left\Vert\,\underline{u}\,\right\Vert^2} $

and

$\displaystyle \mathbf{P}_{\underline{u}}\, \underline{x}= \underline{u}\,\frac{... ...<\underline{u},\underline{x}\right>}{\left\Vert\,\underline{u}\,\right\Vert^2} $

specifically projects $ \underline{x}$ onto $ \underline{u}$. Since the projection is orthogonal, we have

$\displaystyle \left<\underline{x}-\mathbf{P}_{\underline{u}}\underline{x},\unde... ...}-\mathbf{P}_{\underline{u}})\underline{x},\underline{u}\right>=\underline{0}. $

We may interpret $ (\mathbf{I}-\mathbf{P}_{\underline{u}})\underline{x}$ as the difference vector between $ \underline{x}$ and $ \mathbf{P}_{\underline{u}}\underline{x}$, its orthogonal projection onto $ \underline{u}$, since

$\displaystyle (\mathbf{I}-\mathbf{P}_{\underline{u}})\underline{x}+ \mathbf{P}_{\underline{u}}\underline{x}= \underline{x} $

and we have $ (\mathbf{I}-\mathbf{P}_{\underline{u}})\underline{x}\perp \mathbf{P}_{\underline{u}}\underline{x}$ by definition of the orthogonal projection. Consequently, the projection onto $ \underline{u}$ minus this difference vector gives a reflection of the vector $ \underline{x}$ about $ \underline{u}$:

$\displaystyle \underline{y}= \mathbf{P}_{\underline{u}}\underline{x}- (\mathbf{... ...line{u}})\underline{x}= (2\mathbf{P}_{\underline{u}}- \mathbf{I})\underline{x} $

Thus, $ \underline{y}$ is obtained by reflecting $ \underline{x}$ about $ \underline{u}$--a so-called Householder reflection.

Next Section:
Most General Lossless Feedback Matrices
Previous Section:
Householder Feedback Matrix