Impedance Networks
The concept of impedance is central in classical electrical
engineering. The simplest case is Ohm's Law for a resistor
![]() :
:
Thanks to the Laplace transform [449]2.15(or Fourier transform [451]),
the concept of impedance easily extends to masses and springs as well.
We need only allow impedances to be frequency-dependent. For
example, the Laplace transform of Newton's ![]() yields, using the
differentiation theorem for Laplace transforms [449],
yields, using the
differentiation theorem for Laplace transforms [449],
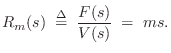
![\begin{eqnarray*}
R_k(s) &=& \frac{k}{s}\\ [5pt]
R_k(j\omega) &=& \frac{k}{j\omega}.
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img362.png)
The important benefit of this frequency-domain formulation of impedance is that it allows every interconnection of masses, springs, and dashpots (every RLC equivalent circuit) to be treated as a simple resistor network, parametrized by frequency.
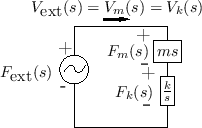 |
As an example, Fig.1.11 gives the impedance diagram corresponding to the equivalent circuit in Fig.1.10. Viewing the circuit as a (frequency-dependent) resistor network, it is easy to write down, say, the Laplace transform of the force across the spring using the voltage divider formula:
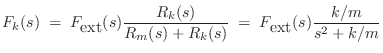
Next Section:
Wave Digital Filters
Previous Section:
Equivalent Circuits




















