Free Books
   Free Books    Physical Audio Signal Processing  

Interpolation of Uniformly Spaced Samples

In the uniformly sampled case ($ x_k=kT$ for some sampling interval $ T$), a Lagrange interpolator can be viewed as a Finite Impulse Response (FIR) filter [449]. Such filters are often called fractional delay filters [267], since they are filters providing a non-integer time delay, in general. Let $ h(n)$ denote the impulse response of such a fractional-delay filter. That is, assume the interpolation at point $ x$ is given by

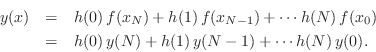
\begin{eqnarray*} y(x) &=& h(0)\,f(x_N) + h(1)\,f(x_{N-1}) + \cdots h(N)\,f(x_0)\\ &=& h(0)\,y(N) + h(1)\,y(N-1) + \cdots h(N)\,y(0). \end{eqnarray*}

where we have set $ T=1$ for simplicity, and used the fact that $ y(x_k)=f(x_k)$ for $ k=0,1,\ldots,N$ in the case of ``true interpolators'' that pass through the given samples exactly. For best results, $ y(x)$ should be evaluated in a one-sample range centered about $ x=N/2$. For delays outside the central one-sample range, the coefficients can be shifted to translate the desired delay into that range.

Next Section:
Fractional Delay Filters
Previous Section:
Large Delay Changes