The DW and FDTD state-space models are equivalent with respect to
lossy traveling-wave simulation. Figure E.4 shows the flow diagram
for the case of simple attenuation by  per sample of wave
propagation, where
per sample of wave
propagation, where ![$ g\in(0,1]$](http://www.dsprelated.com/josimages_new/pasp/img4741.png) for a passive string.
for a passive string.
Figure E.4:
DW flow diagram in the lossy case.
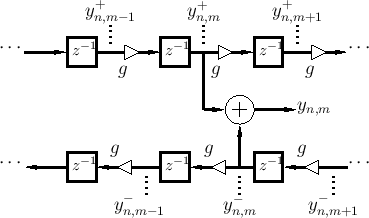 |
The DW state update can be written in this case as
where the loss associated with two time steps has been incorporated
into the chosen subgrid for physical accuracy. (The neglected subgrid
may now be considered lossless.) In changing coordinates to the FDTD
scheme, the gain factor

can remain factored out, yielding
When the input is zero after a particular time, such as in a plucked
or
struck string simulation, the losses can be implemented at the
final output, and only when an output is required,
e.g.,
where
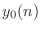
denotes the corresponding lossless simulation. When
there is a general input
signal, the state vector needs to be properly
attenuated by losses. In the DW case, the losses can be lumped at two
points per spatial input and output [
447].
Next Section: State Space SummaryPrevious Section: Boundary Conditions
![]() per sample of wave
propagation, where
per sample of wave
propagation, where ![]() for a passive string.
for a passive string.





















